Basics of real analysis

ECON2125/6012 Lecture 4
Fedor Iskhakov

Announcements & Reminders

1. The first test is due before the next lecture!

• The test will be published tomorrow (before midnight on Friday)

• The test will include multiple choice questions (where multiple options can be correct), True/False questions and open response questions where you may need to upload a file

• Please, find the practice test on Wattle and make sure you are comfortable with the setup, including uploading an image/pdf file

• Tests are timed: practice paying attention to the countdown timer

• The deadline for submission of the first test is midnight on Wednesday, August 23

2. I am traveling next week, no face-to-face lecture on August 24!

• DSE summer school and conference

Plan for this lecture

Continuing with revision of fundamental concepts and ideas

1. Sequences

2. Convergence and limits

3. Differentiation, Taylor series

4. Analysis in \(\mathbb{R}^n\)

5. Open and closed sets

6. Continuity of functions

Mainly review of key ideas

Supplementary reading:

• Simon & Blume: 12.1, 12.2, 12.3, 12.4, 12.5 10.1, 10.2, 10.3, 10.4, 13.4

• Sundaram: 1.1.1, 1.1.2, 1.2.1, 1.2.2, 1.2.3, 1.2.7, 1.2.8, 1.4.1

Analysis in \(\mathbb{R}\)

Example

Let \(F(x)\) be a profit function, so for solving profit maximization we have to solve \(f(x)=0\) where \(f(x)=F'(x)\).

Or: we want to solve an equation \(g(x) = y\) for \(x\), equivalently \(f(x) = g(x) - y\)

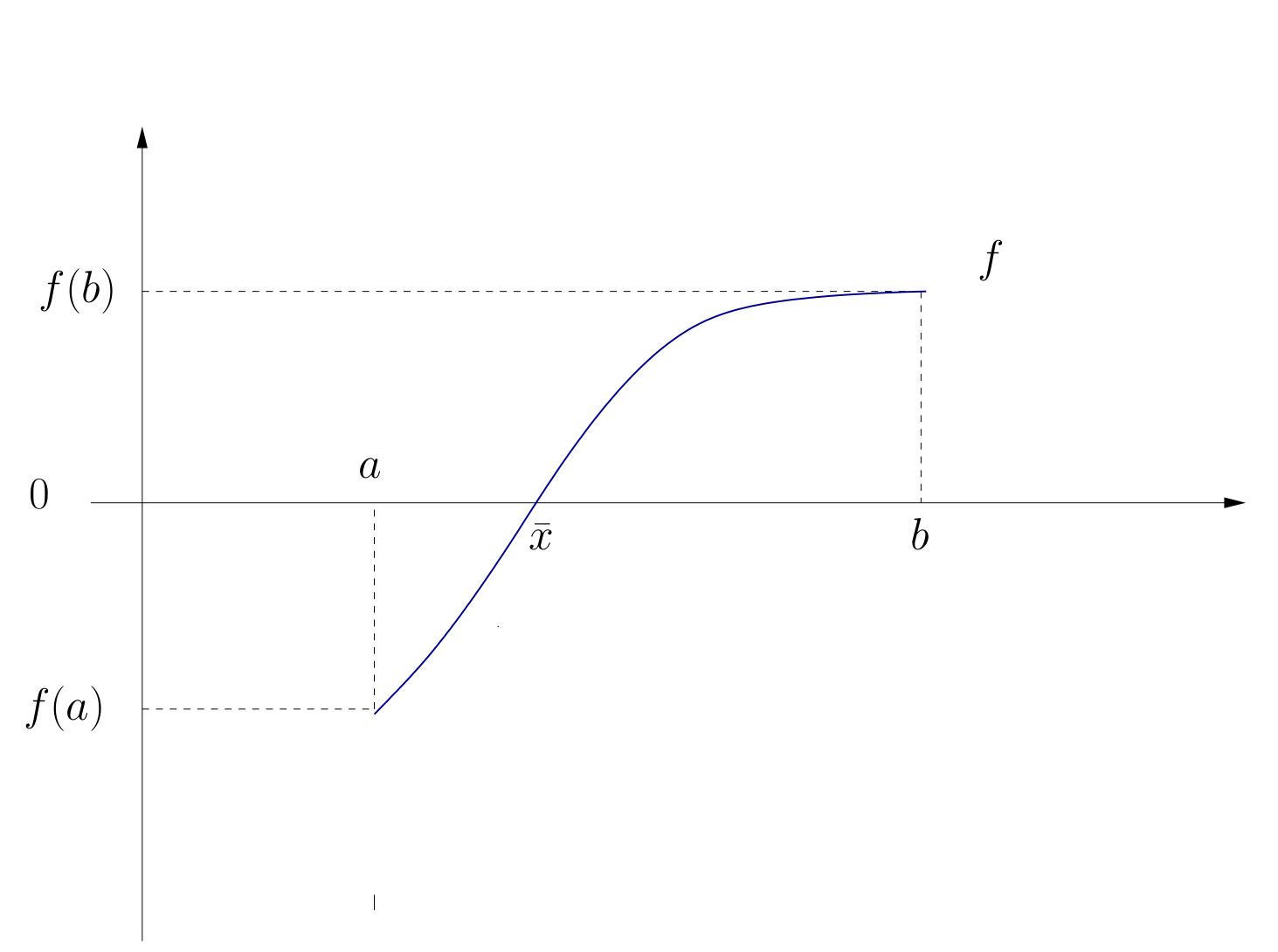
Fig. 31 Existence of a root

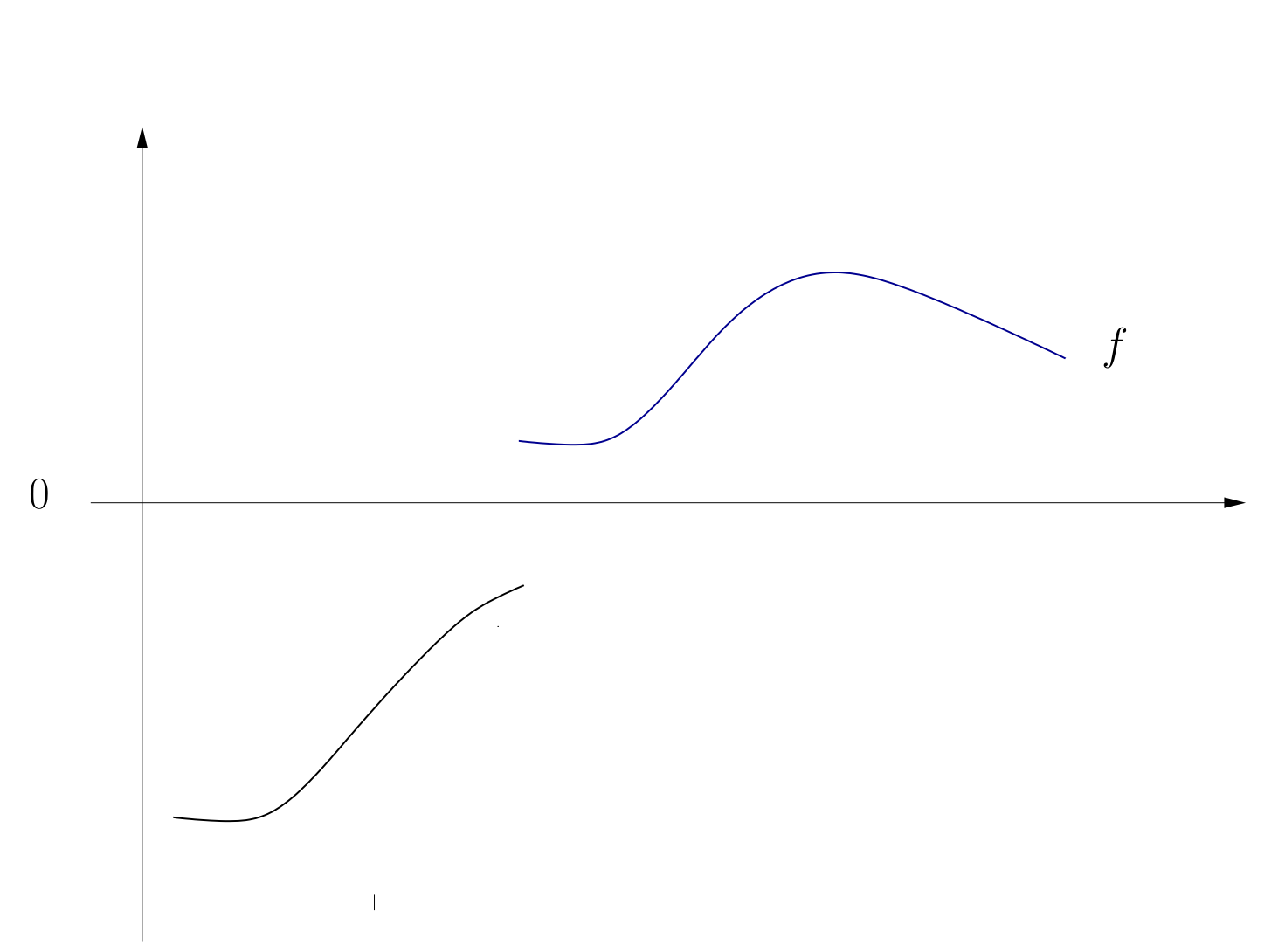
Fig. 32 Non-existence of a root

One answer: a solution exists under certain conditions including continuity.

Questions:

• So how can I tell if \(f\) is continuous?

• Can we weaken the continuity assumption?

• Does this work in multiple dimensions?

• When is the root unique?

• How can we compute it?

These are typical problems in analysis

Bounded sets

Definition

The absolute value of \(x \in \mathbb{R}\) denoted \(|x|\) is \(|x| := \max\{x, -x\}\).

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

def subplots():
    "Custom subplots with axes throught the origin"
    fig, ax = plt.subplots()

    # Set the axes through the origin
    for spine in ['left', 'bottom']:
        ax.spines[spine].set_position('zero')
    for spine in ['right', 'top']:
        ax.spines[spine].set_color('none')
    
    ax.grid()
    return fig, ax

fig, ax = subplots()

ax.set_ylim(-3, 3)
ax.set_yticks((-3, -2, -1, 1, 2, 3))
x = np.linspace(-3, 3, 100)
ax.plot(x, np.abs(x), 'g-', lw=2, alpha=0.7, label=r'$f(x) = |x|$')
ax.plot(x, x, 'k--', lw=2, alpha=0.7, label=r'$f(x) = x$')
ax.legend(loc='lower right')

plt.show()

Fact

For any \(x, y \in \mathbb{R}\), the following statements hold

1. \(|x| \leq y\) if and only if \(-y \leq x \leq y\)

2. \(|x| < y\) if and only if \(-y < x < y\)

3. \(|x| = 0\) if and only if \(x=0\)

4. \(|xy| = |x| |y|\)

5. \(|x+y| \leq |x| + |y|\)

Last inequality is called the triangle inequality

Using these rules, let’s show that if \(x, y, z \in \mathbb{R}\), then

1. \(|x-y| \leq |x| + |y|\)

2. \(|x-y| \leq |x - z| + |z - y|\)

Proof

Hint: \(x-y = x-z+z-y\)

Definition

\(A \subset \mathbb{R}\) is called bounded if \(\exists \; M \in \mathbb{R}\) s.t. \(|x| \leq M\), all \(x \in A\)

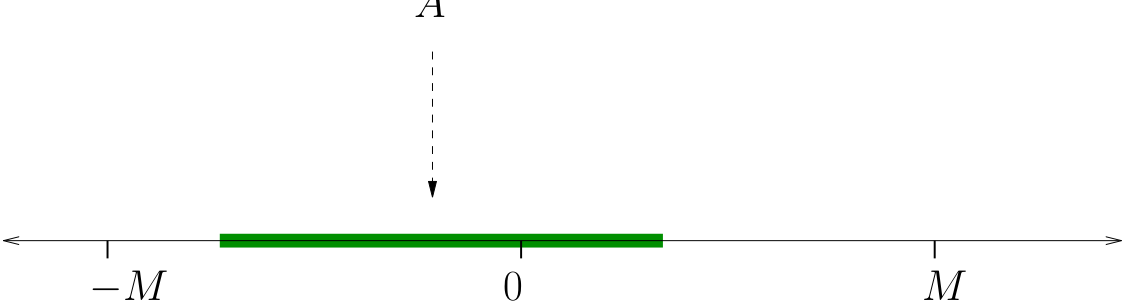
Example

Every finite subset \(A\) of \(\mathbb{R}\) is bounded

Set \(M := \max \{ |a| : a \in A \}\)

Example

\(\mathbb{N}\) is unbounded

For any \(M \in \mathbb{R}\) there is an \(n\) that exceeds it

Example

\((a, b)\) is bounded for any \(a\) and \(b\)

Proof

We have to show that each \(x \in (a, b)\) satisfies \(|x| \leq M := \max\{ |a|, |b| \}\)

\[ x \in (a, b) \iff a < x < b \]

Cases:

1. \(0 \le a \le b \implies x > 0, x = |x| < |b| = b = \max\{|a|,|b|\}\)

2. \(a \le b \le 0 \implies a < x < 0, |x|= -x < -a = |a| = \max\{|a|,|b|\}\)

3. \(a \le 0 \le b \implies\)

\[\begin{split} \begin{cases} |x|<|b|, x \ge 0\\ |x|<|a|, x < 0 \end{cases} \implies |x|< \max\{|a|,|b|\} \text{ from 1. and 2.} \end{split}\]

Fact

If \(A\) and \(B\) are bounded sets then so is \(A \cup B\)

Proof

Let \(A\) and \(B\) be bounded sets and let \(C := A \cup B\)

By definition, \(\exists \, M_A\) and \(M_B\) with

\[ |a| \leq M_A, \text{ all } a \in A, \quad \quad |b| \leq M_B, \text{ all } b \in B \]

Let \(M_C := \max\{M_A , M_B\}\) and fix any \(x \in C\)

\[ x \in C \implies x \in A \text{ or } x \in B \]

\[ \text{therefore } |x| \leq M_A \quad \text{or} \quad |x| \leq M_B \]

\[ \text{therefore } |x| \leq M_C \]

Epsilon-balls (\(\epsilon\)-balls)

Definition

Given \(\epsilon > 0\) and \(a \in \mathbb{R}\), the \(\epsilon\)-ball around \(a\) is

\[ B_{\epsilon}(a) := \{ x \in \mathbb{R} : |a - x| < \epsilon \} \]

Equivalently,

\[ B_\epsilon(a) = \{ x \in \mathbb{R} : a - \epsilon < x < a + \epsilon \} \]

Exercise: Check equivalence

Fact

If \(x\) is in every \(\epsilon\)-ball around \(a\) then \(x=a\)

Proof

Suppose to the contrary that

• \(x\) is in every \(\epsilon\)-ball around \(a\) and yet \(x \ne a\)

Since \(x\) is not \(a\) we must have \(|x-a| > 0\)

Set \(\epsilon := |x-a|\)

Since \(\epsilon > 0\), we have \(x \in B_{\epsilon}(a)\)

This means that \(|x-a| < \epsilon\)

That is, \(|x - a| < |x - a|\)

Contradiction!

Fact

If \(a \ne b\), then \(\exists \; \epsilon > 0\) such that \(B_{\epsilon}(a)\) and \(B_{\epsilon}(b)\) are disjoint.

Proof

Let \(a, b \in \mathbb{R}\) with \(a \ne b\)

If we set \(\epsilon := |a-b|/2\), then \(B_{\epsilon}(a)\) and \(B_\epsilon(b)\) are disjoint

To see this, suppose to the contrary that \(\exists \, x \in B_{\epsilon}(a) \cap B_\epsilon(B)\)

Then \( |x - a| < |a -b|/2\) and \(|x - b| < |a -b|/2\)

But then

\[ |a - b| \leq |a - x| + |x - b| < |a -b|/2 + |a -b|/2 = |a-b| \]

Contradiction!

Sequences

Definition

A sequence is a function from \(\mathbb{N}\) to \(\mathbb{R}\)

To each \(n \in \mathbb{N}\) we associate one \(x_n \in \mathbb{R}\)

Typically written as \(\{x_n\}_{n=1}^{\infty}\) or \(\{x_n\}\) or \(\{x_1, x_2, x_3, \ldots\}\)

Example

• \(\{x_n\} = \{2, 4, 6, \ldots \}\)

• \(\{x_n\} = \{1, 1/2, 1/4, \ldots \}\)

• \(\{x_n\} = \{1, -1, 1, -1, \ldots \}\)

• \(\{x_n\} = \{0, 0, 0, \ldots \}\)

Definition

Sequence \(\{x_n\}\) is called

• bounded if \(\{x_1, x_2, \ldots\}\) is a bounded set

• monotone increasing if \(x_{n+1} \geq x_n\) for all \(n\)

• monotone decreasing if \(x_{n+1} \leq x_n\) for all \(n\)

• monotone if it is either monotone increasing or monotone decreasing

Example

• \(x_n = 1/n\) is monotone decreasing, bounded

• \(x_n = (-1)^n\) is not monotone but is bounded

• \(x_n = 2n\) is monotone increasing but not bounded

Convergence

Let \(a \in \mathbb{R}\) and let \(\{x_n\}\) be a sequence

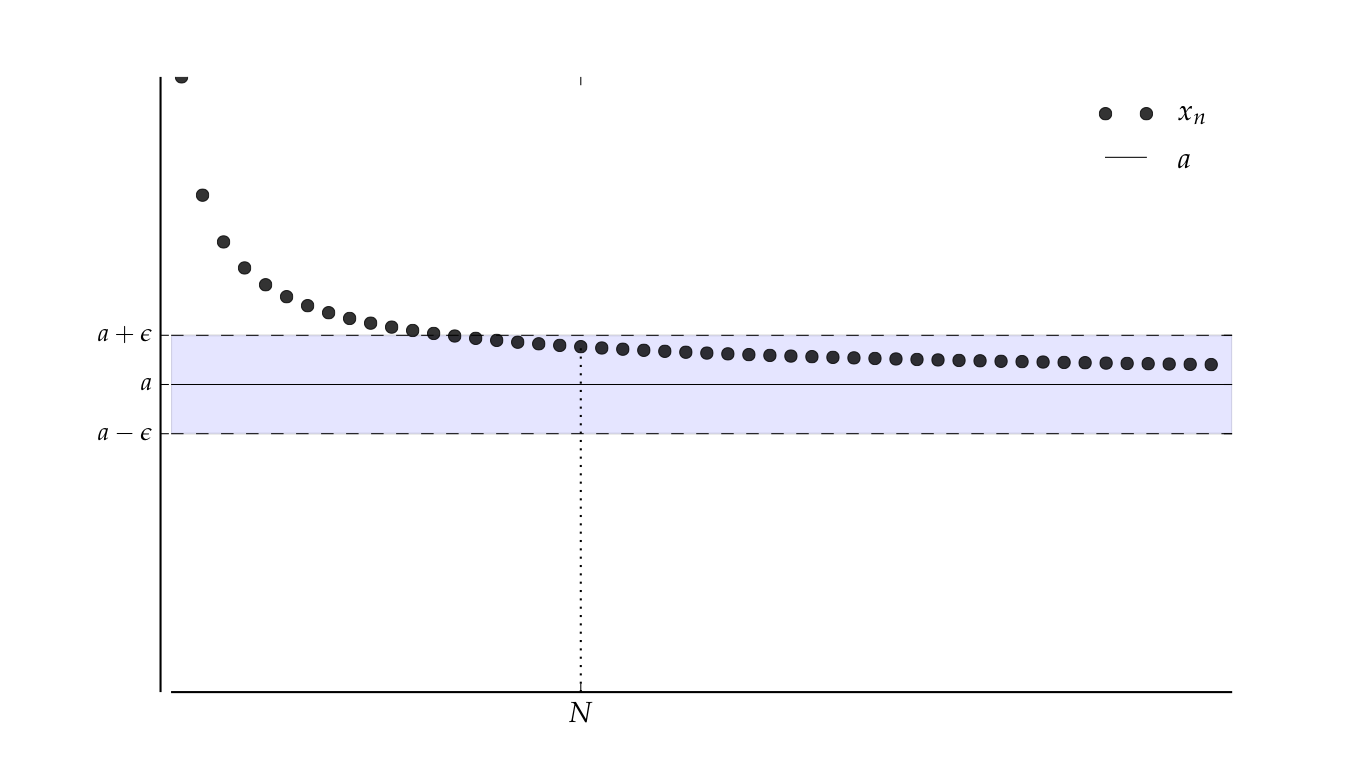
Suppose, for any \(\epsilon > 0\), we can find an \(N \in \mathbb{N}\) such that

\[ x_n \in B_\epsilon(a) \text{ for all } n \geq N \]

Then \(\{x_n\}\) is said to converge to \(a\)

Convergence to \(a\) in symbols,

\[ \forall \, \epsilon > 0, \; \exists \, N \in \mathbb{N} \; \text{ such that } n \geq N \implies x_n \in B_{\epsilon}(a) \]

The sequence \(\{x_n\}\) is eventually in this \(\epsilon\)-ball around \(a\)

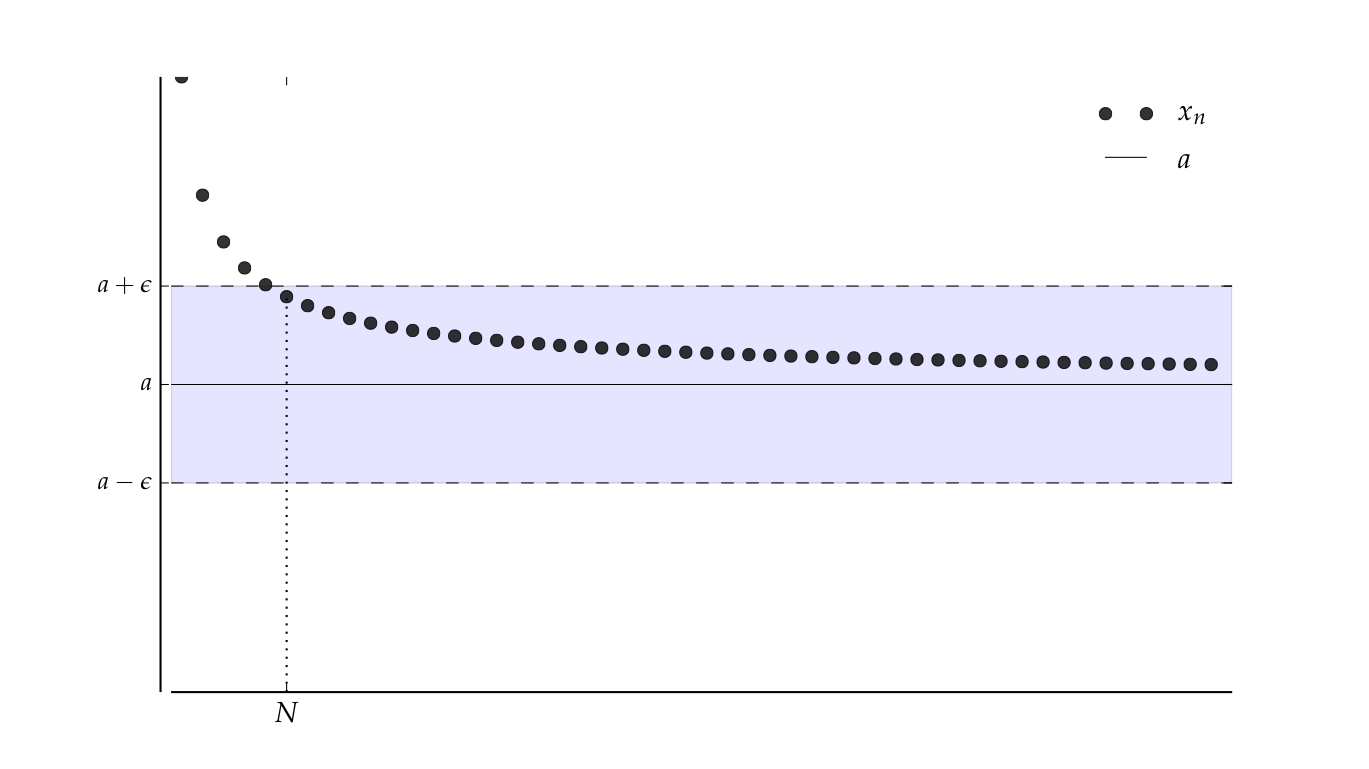
…and this one

…and this one

…and this one

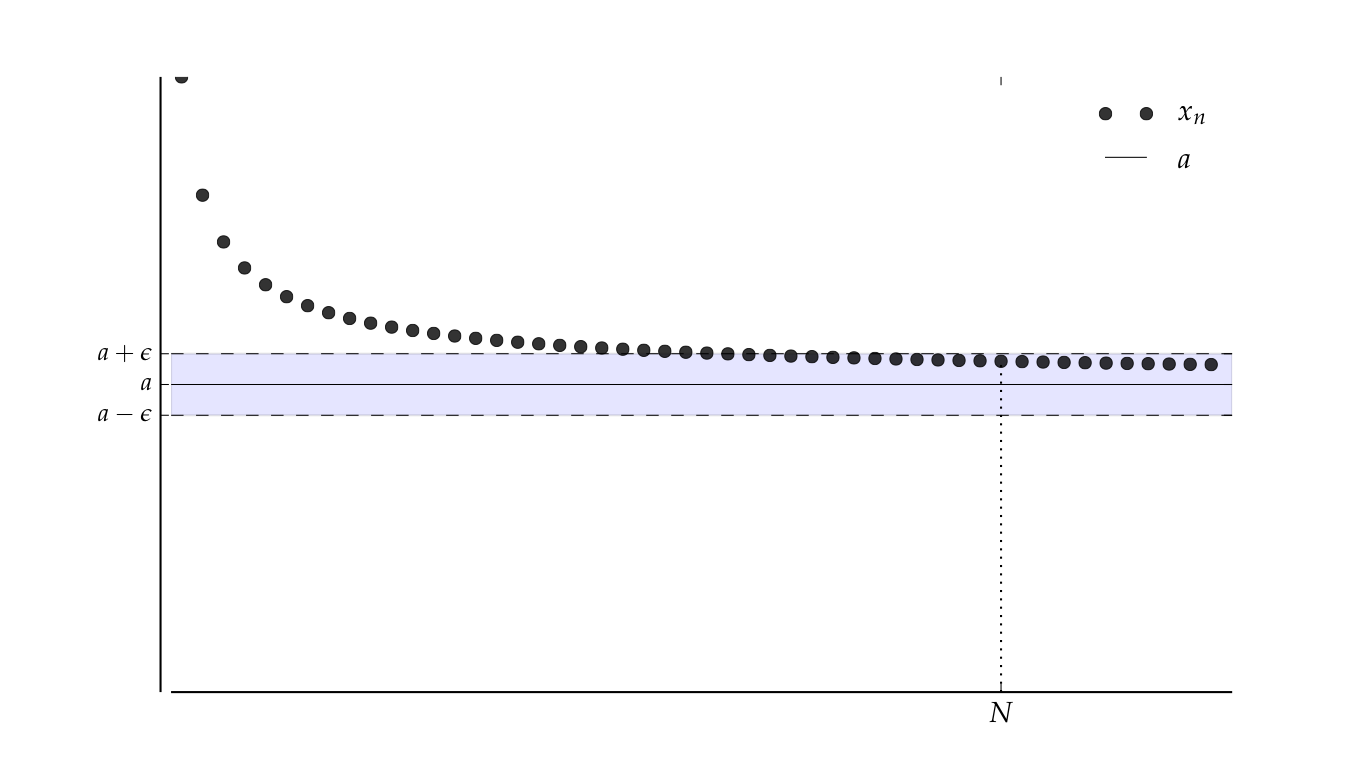
Definition

The point \(a\) is called the limit of the sequence, denoted

\[ x_n \to a \text{ as } n \to \infty \quad \text{ or } \quad \lim_{n \to \infty} x_n = a, \]

if

\[ \forall \, \epsilon > 0, \; \exists \, N \in \mathbb{N} \; \text{ such that } n \geq N \implies x_n \in B_{\epsilon}(a) \]

We call \(\{ x_n \}\) convergent if it converges to some limit in \(\mathbb{R}\)

Example

\(\{x_n\}\) defined by \(x_n = 1 + 1/n\) converges to \(1\):

\[ x_n \to 1 \; \mathrm{as} \; n \to \infty \]

\[ \lim_{n \to \infty} x_n = 1 \]

To prove this must show that \(\forall \, \epsilon > 0\), there is an \(N \in \mathbb{N}\) such that

\[ n \geq N \implies |x_n - 1| < \epsilon \]

To show this formally we need to come up with an “algorithm”

1. You give me any \(\epsilon > 0\)

2. I respond with an \(N\) such that equation above holds

In general, as \(\epsilon\) shrinks, \(N\) will have to grow

Proof

Here’s how to do this for the case \(1 + 1/n\) converges to \(1\)

First pick an arbitrary \(\epsilon > 0\)

Now we have to come up with an \(N\) such that

\[ n \geq N \implies |1 + 1/n - 1| < \epsilon \]

Let \(N\) be the first integer greater than \( 1/\epsilon\)

Then

\[ n \geq N \implies n > 1/\epsilon \implies 1/n < \epsilon \implies |1 + 1/n - 1| < \epsilon \]

Remark: Any \(N' > N\) would also work

Example

The sequence \(x_n = 2^{-n}\) converges to \(0\) as \(n \to \infty\)

Proof

Must show that, \(\forall \, \epsilon > 0\), \(\exists \, N \in \mathbb{N}\) such that

\[ n \geq N \implies |2^{-n} - 0| < \epsilon \]

So pick any \(\epsilon > 0\), and observe that

\[ |2^{-n} - 0| < \epsilon \; \iff \; 2^{-n} < \epsilon \; \iff \; n > - \frac{\ln \epsilon}{\ln 2} \]

Hence we take \(N\) to be the first integer greater than \(- \ln \epsilon / \ln 2\)

Then

\[ n \geq N \implies n > -\frac{\ln \epsilon}{\ln 2} \implies |2^{-n} - 0| < \epsilon \]

What if we want to show that \(x_n \to a\) fails?

To show convergence fails we need to show the negation of

\[ \forall \,\; \epsilon > 0, \;\; \exists \,\; N \in \mathbb{N} \;\mathrm{such\;that}\; n \geq N \implies x_n \in B_{\epsilon}(a) \]

Negation: there is an \(\epsilon > 0\) where we can’t find any such \(N\)

More specifically, \(\exists \, \epsilon > 0\) such that, which ever \(N \in \mathbb{N}\) we look at, there’s an \(n \geq N\) with \(x_n\) outside \(B_{\epsilon}(a)\)

One way to say this: there exists a \(B_\epsilon(a)\) such that \(x_n \notin B_\epsilon(a)\) again and again as \(n \to \infty\).

This is the kind of picture we’re thinking of

Show code cell source Hide code cell source

from __future__ import division
import matplotlib.pyplot as plt
import numpy as np

from matplotlib import rc
rc('font',**{'family':'serif','serif':['Palatino']})
rc('text', usetex=True)

N = 80
epsilon = 0.15
a = 1

def x(n):
    return 1 + 1/(n**(0.7)) - 0.3 * (n % 8 == 0)
def subplots(fs):
    "Custom subplots with axes throught the origin"
    fig, ax = plt.subplots(figsize=fs)
    # Set the axes through the origin
    for spine in ['left', 'bottom']:
        ax.spines[spine].set_position('zero')
    for spine in ['right', 'top']:
        ax.spines[spine].set_color('none')
    return fig, ax

fig, ax = subplots((9, 5))  

xmin, xmax = 0.5, N+1
ax.set_xlim(xmin, xmax)
ax.set_ylim(0, 2)

n = np.arange(1, N+1)
ax.set_xticks([])
ax.plot(n, x(n), 'ko', label=r'$x_n$', alpha=0.8)

ax.hlines(a, xmin, xmax, color='k', lw=0.5, label='$a$')
ax.hlines([a - epsilon, a + epsilon], xmin, xmax, color='k', lw=0.5, linestyles='dashed')

ax.fill_between((xmin, xmax), a - epsilon, a + epsilon, facecolor='blue', alpha=0.1)

ax.set_yticks((a - epsilon, a, a + epsilon))
ax.set_yticklabels((r'$a - \epsilon$', r'$a$', r'$a + \epsilon$'))

ax.legend(loc='upper right', frameon=False, fontsize=14)
plt.show()

Example

The sequence \(x_n = (-1)^n\) does not converge to any \(a \in \mathbb{R}\)

Proof

This is what we want to show

\[ \exists \,\; \epsilon > 0 \;\text{ such that } x_n \notin B_{\epsilon}(a) \text{ infinitely many times as } n \to \infty \]

Since it’s a “there exists”, we need to come up with such an \(\epsilon\)

Let’s try \(\epsilon = 0.5\), so that

\[ B_\epsilon(a) = \{ x \in \mathbb{R} : |x - a| < 0.5 \} = (a-0.5, a+0.5 ) \]

We have:

• If \(n\) is odd then \(x_n = -1\) when \(n > N\) for any \(N\).

• If \(n\) is even then \(x_n = 1\) when \(n > N\) for any \(N\).

Therefore even if \(a=1\) or \(a=-1\), \(\{x_n\}\) not in \(B_\epsilon(a)\) infinitely many times as \(n \to \infty\). It holds for all other values of \(a \in \mathbb{R}\).

Properties of Limits

Fact

Let \(\{x_n\}\) be a sequence in \(\mathbb{R}\) and let \(a \in \mathbb{R}\). Then as \(n \to \infty\)

\[ x_n \to a \iff |x_n - a| \to 0 \]

Proof

Compare the definitions:

• \(x_n \to a\) \(\iff\) \(\forall \, \epsilon > 0\), \(\exists \, N \in \mathbb{N}\) s.t. \(|x_n - a| < \epsilon\)

• \(|x_n - a| \to 0\) \(\iff\) \(\forall \, \epsilon > 0\), \(\exists \, N \in \mathbb{N}\) s.t. \(||x_n - a| - 0| < \epsilon\)

Clearly these statements are equivalent

Fact

Each sequence in \(\mathbb{R}\) has at most one limit

Proof

Suppose instead that \(x_n \to a \text{ and } x_n \to b \text{ with } a \ne b \)

Take disjoint \(\epsilon\)-balls around \(a\) and \(b\)

Since \(x_n \to a\) and \(x_n \to b\),

• \(\exists \; N_a\) s.t. \(n \geq N_a \implies x_n \in B_{\epsilon}(a)\)

• \(\exists \; N_b\) s.t. \(n \geq N_b \implies x_n \in B_{\epsilon}(b)\)

But then \(n \geq \max\{N_a, N_b\} \implies \) \(x_n \in B_{\epsilon}(a)\) and \(x_n \in B_{\epsilon}(b)\)

Contradiction, as the balls are assumed disjoint

Fact

Every convergent sequence is bounded

Proof

Let \(\{x_n\}\) be convergent with \(x_n \to a\)

Fix any \(\epsilon > 0\) and choose \(N\) s.t. \(x_n \in B_{\epsilon}(a)\) when \(n \geq N\)

Regarded as sets,

\[ \{x_n\} \subset \{x_1, \ldots, x_{N-1}\} \cup B_{\epsilon}(a) \]

Both of these sets are bounded

• First because finite sets are bounded

• Second because \(B_{\epsilon}(a)\) is bounded

Further, finite unions of bounded sets are bounded

Operations with limits

Here are some basic tools for working with limits

Fact

If \(x_n \to x\) and \(y_n \to y\), then

1. \(x_n + y_n \to x + y\)

2. \(x_n y_n \to x y\)

3. \(x_n /y_n \to x / y\) when \(y_n\) and \(y\) are \(\ne 0\)

4. \(x_n \leq y_n\) for all \(n \implies x \leq y\)

Let’s check that \(x_n \to x\) and \(y_n \to y\) implies \(x_n + y_n \to x + y\)

Proof

Fix \(\epsilon > 0\)

Need to find \(N \in \mathbb{N}\) such that

\[ n \geq N \; \implies \; |(x_n + y_n) - (x + y)| < \epsilon \]

Note that

• \(|(x_n + y_n) - (x + y)| \leq |x_n - x| + |y_n - y|\) by triangle inequality

• \(\exists N_x \in \mathbb{N}\) such that \(n \geq N_x \implies |x_n - x| < \epsilon/2\) by definition of the limit

• \(\exists N_y \in \mathbb{N}\) such that \(n \geq N_y \implies |y_n - y| < \epsilon/2\) by definition of the limit as well

Take \(N := \max\{N_x, N_y\}\)

Combining the inequalities above concludes the proof.

Let’s also check the claim that \(x_n \to x\), \(y_n \to y\) and \(x_n \leq y_n\) for all \(n \in \mathbb{N}\) implies \(x \leq y\)

Proof

Suppose instead that \(x > y\)

Take disjoint \(\epsilon\)-balls \(B_\epsilon(x)\) and \(B_\epsilon(y)\) around these points

There exists an \(n\) such that \(x_n \in B_\epsilon(x)\) and \(y_n \in B_\epsilon(y)\)

But then \(x_n > y_n\), a contradiction

In words: “Weak inequalities are preserved under limits”

Here’s another property of limits, called the “squeeze theorem”

Fact

Let \(\{x_n\}\) \(\{y_n\}\) and \(\{z_n\}\) be sequences in \(\mathbb{R}\). If

1. \(x_n \leq y_n \leq z_n\) for all \(n \in \mathbb{N}\)

2. \(x_n \to a\) and \(z_n \to a\)

then \(y_n \to a\) also holds

Proof

Pick any \(\epsilon > 0\)

We can choose an

• \(N_x \in \mathbb{N}\) such that \(n \geq N_x \implies x_n \in B_\epsilon(a)\)

• \(N_z \in \mathbb{N}\) such that \(n \geq N_z \implies z_n \in B_\epsilon(a)\)

Exercise: Show that \(n \geq \max\{N_x, N_z\} \implies y_n \in B_\epsilon(a)\)

Infinite Sums

Definition

Let \(\{x_n\}\) be a sequence in \(\mathbb{R}\)

Then the infinite sum of \(\sum_{n=1}^{\infty} x_n\) is defined by

\[ \sum_{n=1}^{\infty} x_n := \lim_{k\to \infty} \sum_{n=1}^k x_n \]

Thus, \(\sum_{n=1}^{\infty} x_n\) is defined as the limit, if it exists, of \(\{y_k\}\) where

\[ y_k := \sum_{n=1}^k x_n \]

Other notation:

\[ \sum_n x_n, \quad \sum_{n \geq 1} x_n, \quad \sum_{n \in \mathbb{N}} x_n, \quad \text{etc.} \]

Example

If \(x_n = \alpha^n\) for \(\alpha \in (0, 1)\), then

\[ \sum_{n=1}^{\infty} x_n = \lim_{k\to \infty} \sum_{n=1}^k \alpha^n = \lim_{k\to \infty} \alpha \frac{1 - \alpha^k}{1 - \alpha} = \frac{\alpha}{1 - \alpha} \]

Exercise: show that \(\sum_{n=1}^k \alpha^n = \alpha \frac{1 - \alpha^k}{1 - \alpha}\).

Example

If \(x_n = (-1)^n\) the limit fails to exist because

\[\begin{split} y_k = \sum_{n=1}^k x_n = \begin{cases} 0 & \text{if $k$ is even} \\ -1 & \text{otherwise} \end{cases} \end{split}\]

Fact

If \(\{x_n\}\) is nonnegative and \(\sum_n x_n < \infty\), then \(x_n \to 0\)

Proof

Suppose to the contrary that \(x_n \to 0\) fails

Then
\(\exists \; \epsilon > 0\) and \(N\) such that \(x_n \notin B_\epsilon(0)\) for \(n>N\) infinitely many times as \(n \to \infty\)

Because \(x_n\) is nonnegative, \(x_n \notin B_\epsilon(0) \implies x_n > \epsilon\)

But then \(\sum_{n = N}^{N+k} x_n > k \epsilon \to \infty\) as \(k \to \infty\)

In other words, \(\sum_{n \ge N} x_n\) cannot be finite — contradiction

Cauchy Sequences

Informal definition: Cauchy sequences are those where \(|x_n - x_{n+1}|\) gets smaller and smaller

Example

Sequences generated by iterative methods for solving nonlinear equations often have this property

Show code cell source Hide code cell source

f = lambda x: -4*x**3+5*x+1
g = lambda x: -12*x**2+5

def newton(fun,grad,x0,tol=1e-6,maxiter=100,callback=None):
    '''Newton method for solving equation f(x)=0
    with given tolerance and number of iterations.
    Callback function is invoked at each iteration if given.
    '''
    for i in range(maxiter):
        x1 = x0 - fun(x0)/grad(x0)
        err = abs(x1-x0)
        if callback != None: callback(err=err,x0=x0,x1=x1,iter=i)
        if err<tol: break
        x0 = x1
    else:
        raise RuntimeError('Failed to converge in %d iterations'%maxiter)
    return (x0+x1)/2

def print_err(iter,err,**kwargs):
    x = kwargs['x'] if 'x' in kwargs.keys() else kwargs['x0']
    print('{:4d}:  x = {:14.8f}    diff = {:14.10f}'.format(iter,x,err))

print('Newton method')
res = newton(f,g,x0=123.45,callback=print_err,tol=1e-10)

Newton method
   0:  x =   123.45000000    diff =  41.1477443465
   1:  x =    82.30225565    diff =  27.4306976138
   2:  x =    54.87155804    diff =  18.2854286376
   3:  x =    36.58612940    diff =  12.1877193931
   4:  x =    24.39841001    diff =   8.1212701971
   5:  x =    16.27713981    diff =   5.4083058492
   6:  x =    10.86883396    diff =   3.5965889909
   7:  x =     7.27224497    diff =   2.3839931063
   8:  x =     4.88825187    diff =   1.5680338561
   9:  x =     3.32021801    diff =   1.0119341175
  10:  x =     2.30828389    diff =   0.6219125117
  11:  x =     1.68637138    diff =   0.3347943714
  12:  x =     1.35157701    diff =   0.1251775194
  13:  x =     1.22639949    diff =   0.0188751183
  14:  x =     1.20752437    diff =   0.0004173878
  15:  x =     1.20710698    diff =   0.0000002022
  16:  x =     1.20710678    diff =   0.0000000000

Cauchy sequences “look like” they are converging to something

A key axiom of analysis is that such sequences do converge to something — details follow

Definition

A sequence \(\{x_n\}\) is called Cauchy if \(\forall \; \epsilon > 0, \;\; \exists \; N \in \mathbb{N}\) such that

\[ n \geq N \text{ and } \forall j \geq 1 \;\; \implies |x_n - x_{n+j}| < \epsilon \]

Example

\(\{x_n\}\) defined by \(x_n = \alpha^n\) where \(\alpha \in (0, 1)\) is Cauchy

Proof

For any \(n , j\) we have

\[ |x_n - x_{n+j}| = |\alpha^n - \alpha^{n+j}| = \alpha^n |1 - \alpha^j| \leq \alpha^n \]

Fix \(\epsilon > 0\)

We can show that \(n > \log(\epsilon) / \log(\alpha) \implies \alpha^n < \epsilon\)

Hence any integer \(N > \log(\epsilon) / \log(\alpha)\) the sequence is Cauchy by definition.

Fact

For any sequence the following equivalence holds: convergent \(\iff\) Cauchy

Proof

Proof of \(\implies\):

Let \(\{x_n\}\) be a sequence converging to some \(a \in \mathbb{R}\)

Fix \(\epsilon > 0\)

We can choose \(N\) s.t.

\[ n \geq N \;\; \implies \;\; |x_n - a | < \frac{\epsilon}{2} \]

For this \(N\) we have \(n \geq N\) and \(j \geq 1\) implies

\[ |x_n - x_{n+j}| \leq |x_n - a| + |x_{n+j} - a| < \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon \]

Proof of \(\Leftarrow\):

This is basically an axiom in the definition of \(\mathbb{R}\)

Either

1. We assume it, or

2. We assume something else that’s essentially equivalent

Implications:

• There are no “gaps” in the real line

• To check \(\{x_n\}\) converges to something we just need to check Cauchy property

Fact

Every bounded monotone sequence in \(\mathbb{R}\) is convergent

Sketch of the proof:

Suffices to show that \(\{x_n\}\) is Cauchy

Suppose not

Then no matter how far we go down the sequence we can find another jump of size \(\epsilon > 0\)

Since monotone, all the jumps are in the same direction

But then \(\{x_n\}\) not bounded — a contradiction

Full proof: See any text on analysis

Subsequences

Definition

A sequence \(\{x_{n_k} \}\) is called a subsequence of \(\{x_n\}\) if

1. \(\{x_{n_k} \}\) is a subset of \(\{x_n\}\)

2. the indices \(n_k\) are strictly increasing

Example

\[ \{x_n\} = \{x_1, x_2, x_3, x_4, x_5, \ldots\} \]

\[ \{x_{n_k}\} = \{x_2, x_4, x_6, x_8 \ldots\} \]

In this case

\[ \{n_k\} = \{n_1, n_2, n_3, \ldots\} = \{2, 4, 6, \ldots\} \]

Example

\(\{\frac{1}{1}, \frac{1}{3}, \frac{1}{5},\ldots\}\) is a subsequence of \(\{\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots\}\)

\(\{\frac{1}{1}, \frac{1}{2}, \frac{1}{3},\ldots\}\) is a subsequence of \(\{\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots\}\)

\(\{\frac{1}{2}, \frac{1}{2}, \frac{1}{2},\ldots\}\) is not a subsequence of \(\{\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots\}\)

Fact

Every sequence has a monotone subsequence

Proof omitted

Example

The sequence \(x_n = (-1)^n\) has monotone subsequence

\[ \{x_2, x_4, x_6, \ldots \} = \{1, 1, 1, \ldots \} \]

This leads us to the famous Bolzano-Weierstrass theorem, to be used later when we discuss optimization.

Fact: Bolzano-Weierstrass theorem

Every bounded sequence in \(\mathbb{R}\) has a convergent subsequence

Proof

Let \(\{x_n\}\) be a bounded sequence

There exists a monotone subsequence

• which is itself a bounded sequence (why?)

• and hence both monotone and bounded

Every bounded monotone sequence converges

Hence \(\{x_n\}\) has a convergent subsequence

Derivatives

Definition

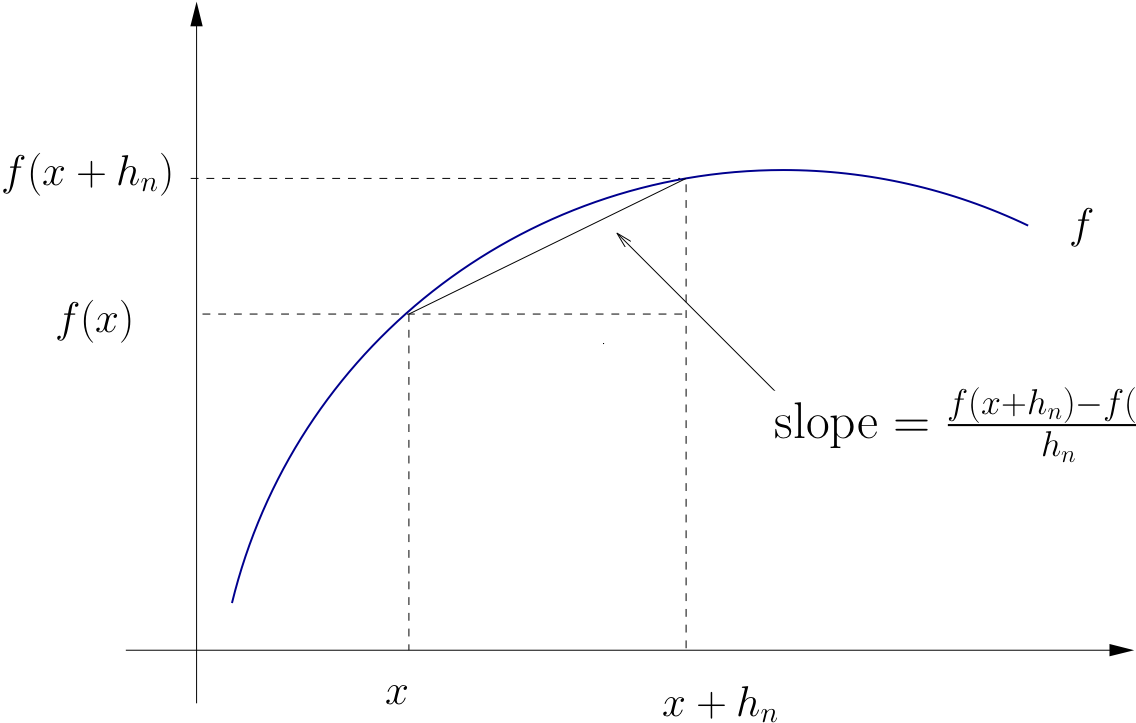
Let \(f \colon (a, b) \to \mathbb{R}\) and let \(x \in (a, b)\)

Let \(H\) be all sequences \(\{h_n\}\) such that \(h_n \ne 0\) and \(h_n \to 0\)

If there exists a constant \(f'(x)\) such that

\[ \frac{f(x + h_n) - f(x)}{h_n} \to f'(x) \]

for every \(\{h_n\} \in H\), then

• \(f\) is said to be differentiable at \(x\)

• \(f'(x)\) is called the derivative of \(f\) at \(x\)

Example

Let \(f \colon \mathbb{R} \to \mathbb{R}\) be defined by \(f(x) = x^2\)

Fix any \(x \in \mathbb{R}\) and any \(h_n \to 0\) with \(n \to \infty\)

We have

\[ \frac{f(x + h_n) - f(x)}{h_n} = \frac{(x + h_n)^2 - x^2}{h_n} = \]

\[ = \frac{x^2 + 2xh_n + h_n^2 - x^2}{h_n} = 2x + h_n \]

\[ \text{therefore } f'(x) = \lim_{n \to \infty} (2x + h_n) = 2x \]

Example

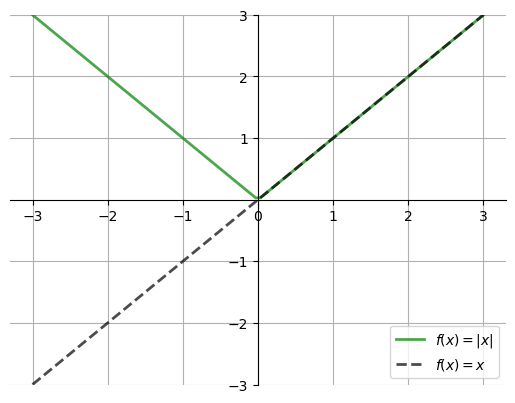
Let \(f \colon \mathbb{R} \to \mathbb{R}\) be defined by \(f(x) = |x|\)

This function is not differentiable at \(x=0\)

Indeed, if \(h_n = 1/n\), then

\[ \frac{f(0 + h_n) - f(0)}{h_n} = \frac{|0 + 1/n| - |0|}{1/n} \to 1 \]

On the other hand, if \(h_n = -1/n\), then

\[ \frac{f(0 + h_n) - f(0)}{h_n} = \frac{|0 - 1/n| - |0|}{-1/n} \to -1 \]

Taylor series

Loosely speaking, if \(f \colon \mathbb{R} \to \mathbb{R}\) is suitably differentiable at \(a\), then

\[ f(x) \approx f(a) + f'(a)(x-a) \]

for \(x\) very close to \(a\),

\[ f(x) \approx f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 \]

on a slightly wider interval, etc.

These are the 1st and 2nd order Taylor series approximations to \(f\) at \(a\) respectively

As the order goes higher we get better approximation

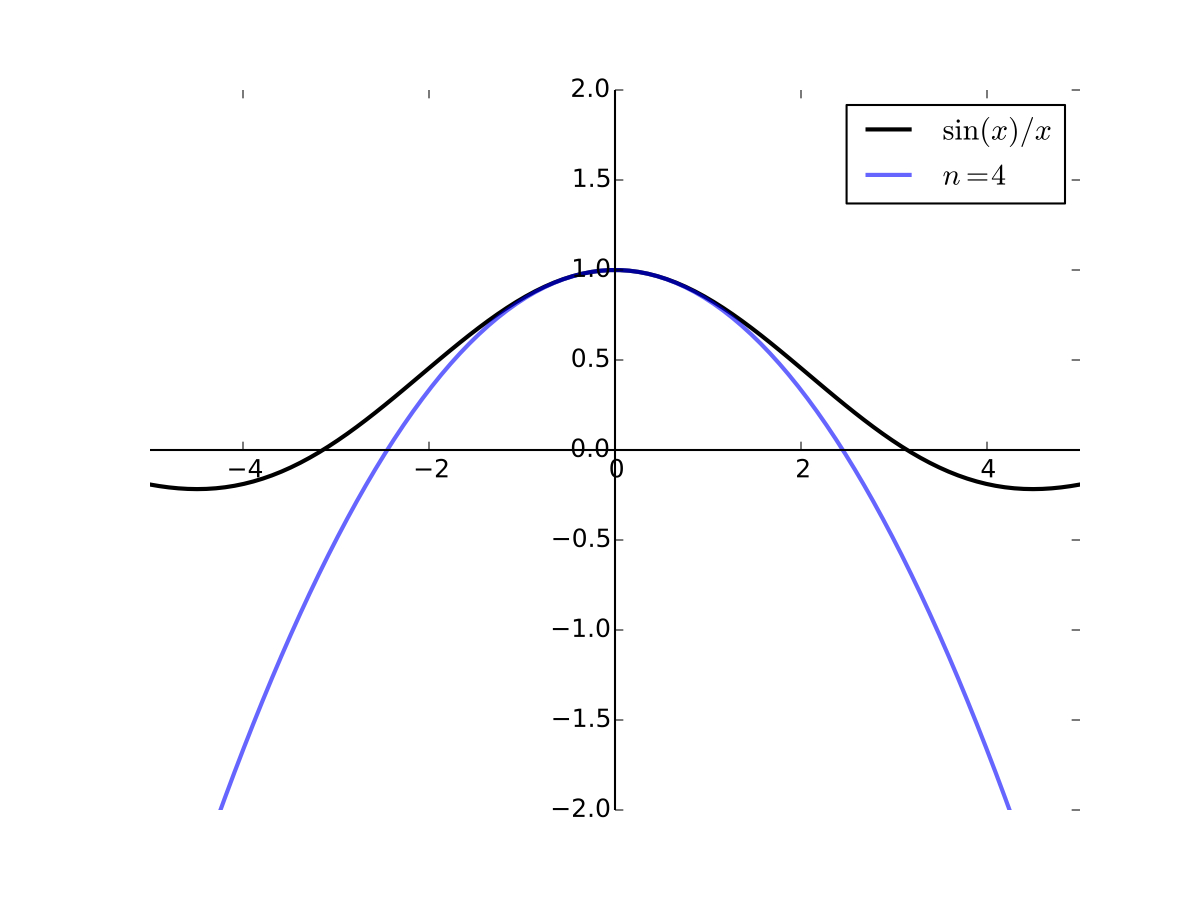
Fig. 33 4th order Taylor series for \(f(x) = \sin(x)/x\) at 0

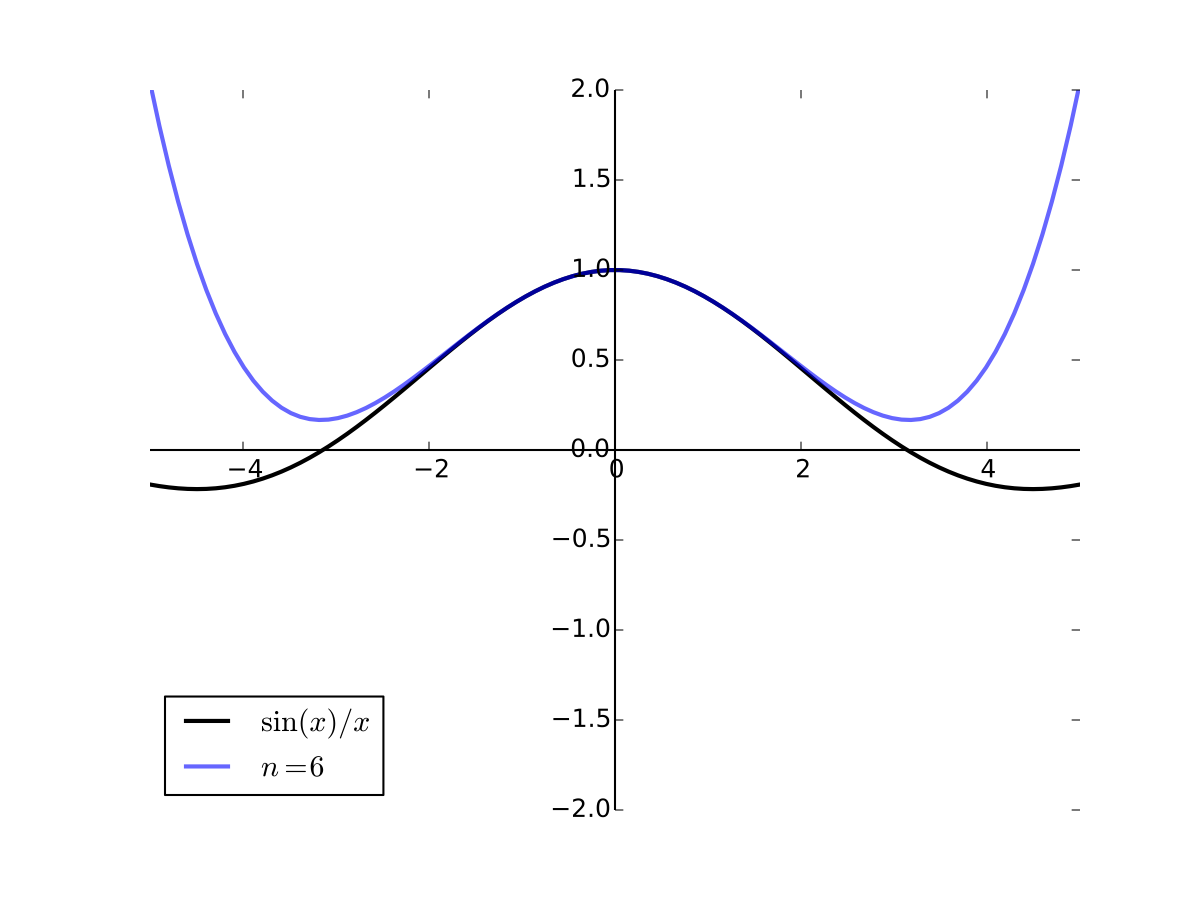
Fig. 34 6th order Taylor series for \(f(x) = \sin(x)/x\) at 0

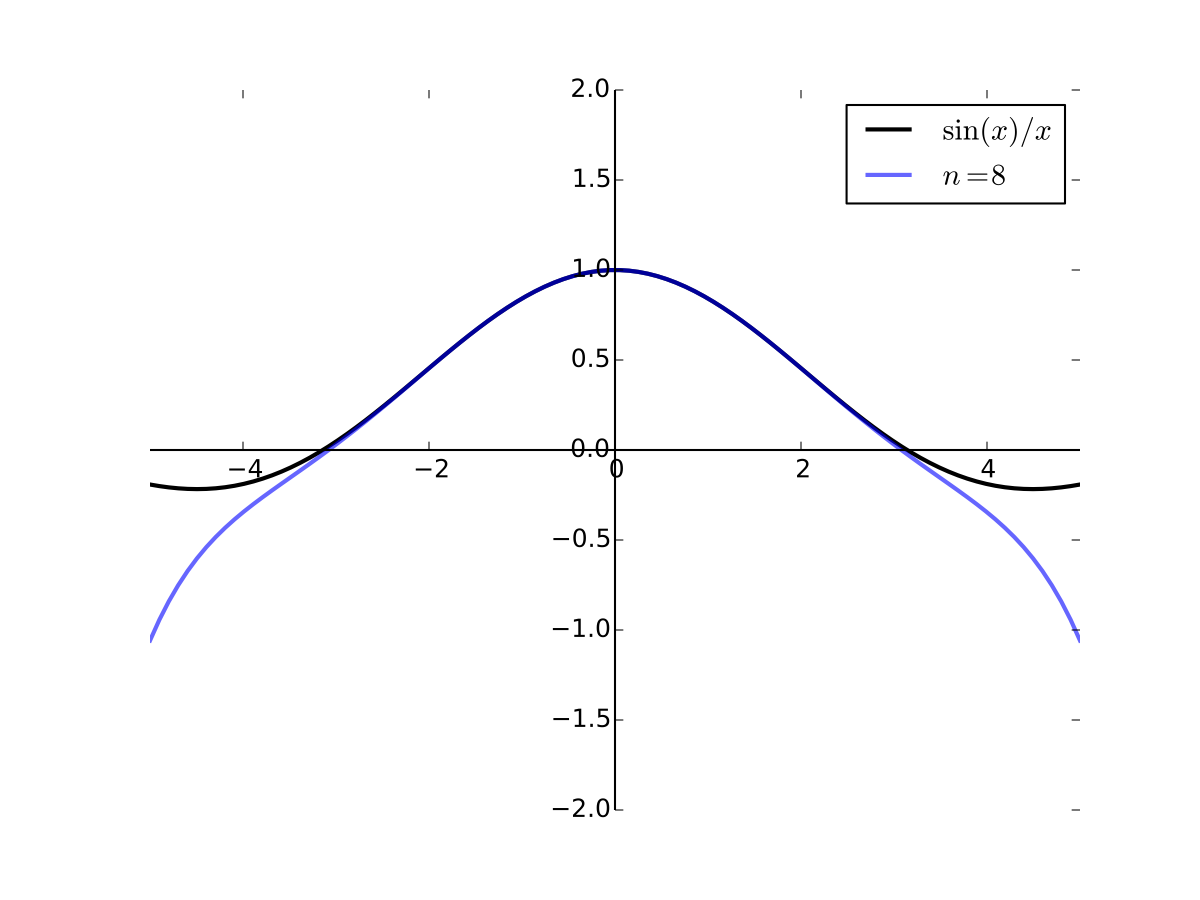
Fig. 35 8th order Taylor series for \(f(x) = \sin(x)/x\) at 0

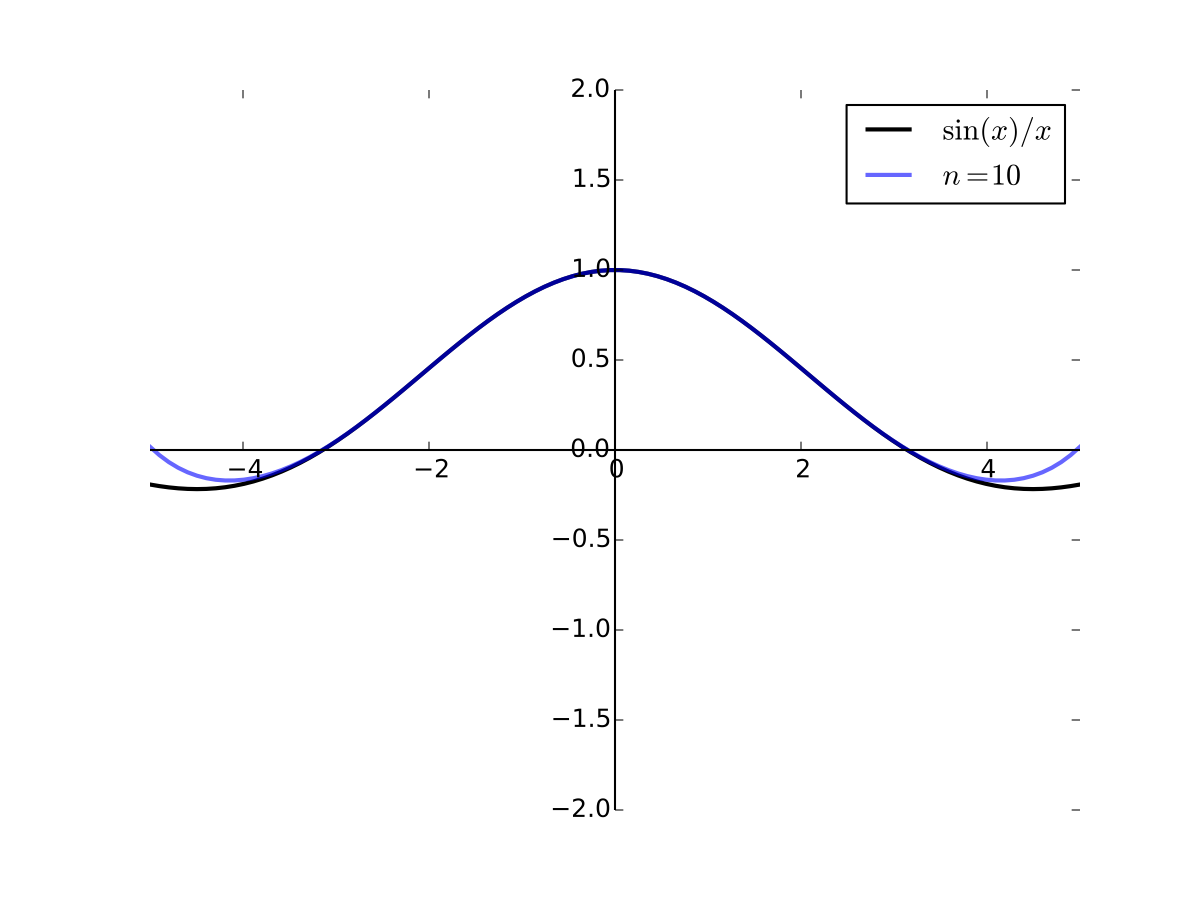
Fig. 36 10th order Taylor series for \(f(x) = \sin(x)/x\) at 0

Analysis in \(\mathbb{R}^K\)

Now we switch from studying points \(x \in \mathbb{R}\) to vectors \({\bf x} \in \mathbb{R}^K\)

• Replace distance \(|x - y|\) with \(\| {\bf x} - {\bf y} \|\)

Many of the same results go through otherwise unchanged

We state the analogous results briefly since

• You already have the intuition from \(\mathbb{R}\)

• Similar arguments, just replacing \(|\cdot|\) with \(\| \cdot \|\)

We’ll spend longer on things that are different

Norm and distance

Definition

The (Euclidean) norm of \({\bf x} \in \mathbb{R}^N\) is defined as

\[ \| {\bf x} \| := \sqrt{{\bf x}' {\bf x} } = \left( \sum_{n=1}^N x_n^2 \right)^{1/2} \]

Interpretation:

• \(\| {\bf x} \|\) represents the length of \({\bf x}\)

• \(\| {\bf x} - {\bf y} \|\) represents distance between \({\bf x}\) and \({\bf y}\)

Fig. 37 Length of red line \(= \sqrt{x_1^2 + x_2^2} =: \|{\bf x}\|\)

\(\| {\bf x} - {\bf y} \|\) represents distance between \({\bf x}\) and \({\bf y}\)

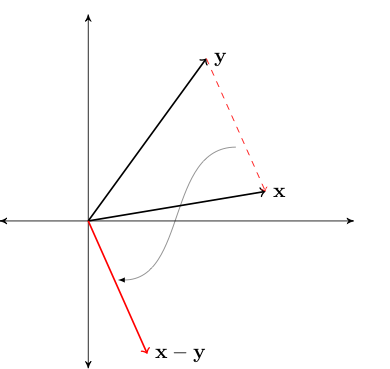
Fig. 38 Length of red line \(= \|{\bf x} - {\bf y}\|\)

Fact

For any \(\alpha \in \mathbb{R}\) and any \({\bf x}, {\bf y} \in \mathbb{R}^N\), the following statements are true:

• \(\| {\bf x} \| \geq 0\) and \(\| {\bf x} \| = 0\) if and only if \({\bf x} = {\bf 0}\)

• \(\| \alpha {\bf x} \| = |\alpha| \| {\bf x} \|\)

• \(\| {\bf x} + {\bf y} \| \leq \| {\bf x} \| + \| {\bf y} \|\) (triangle inequality)

• \(| {\bf x}' {\bf y} | \leq \| {\bf x} \| \| {\bf y} \|\) (Cauchy-Schwarz inequality)

For example, let’s show that \(\| {\bf x} \| = 0 \iff {\bf x} = {\bf 0}\)

First let’s assume that \(\| {\bf x} \| = 0\) and show \({\bf x} = {\bf 0}\)

Since \(\| {\bf x} \| = 0\) we have \(\| {\bf x} \|^2 = 0\) and hence \(\sum_{n=1}^N x^2_n = 0\)

That is \(x_n = 0\) for all \(n\), or, equivalently, \({\bf x} = {\bf 0}\)

Next let’s assume that \({\bf x} = {\bf 0}\) and show \(\| {\bf x} \| = 0\)

This is immediate from the definition of the norm

Bounded sets and \(\epsilon\)-balls

Definition

A set \(A \subset \mathbb{R}^K\) called bounded if

\[ \exists \, M \in \mathbb{R} \; \mathrm{such\;that} \; \|{\bf x}\| \leq M, \quad \forall \; {\bf x} \in A \]

Remarks:

• A generalization of the scalar definition

• When \(K=1\), the norm \(\| \cdot \|\) reduces to \(|\cdot|\)

Fact

If \(A\) and \(B\) are bounded sets then so is \(C := A \cup B\)

Proof: Same as the scalar case — just replace \(|\cdot|\) with \(\| \cdot \|\)

Exercise: Check it

Definition

For \(\epsilon > 0\), the \(\epsilon\)-ball \(B_{\epsilon}({\bf a})\) around \({\bf a} \in \mathbb{R}^K\) is all \({\bf x} \in \mathbb{R}^K\) such that \(\|{\bf a} - {\bf x}\| < \epsilon\)

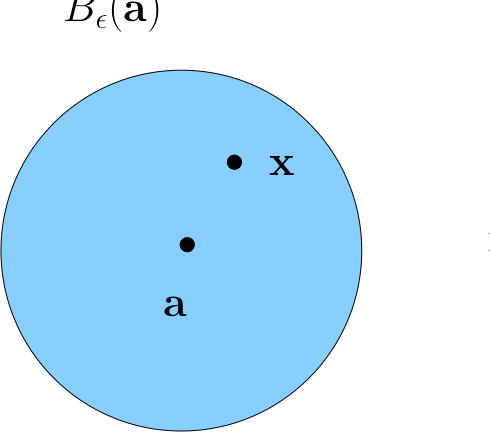
Fact

If \({\bf x}\) is in every \(\epsilon\)-ball around \({\bf a}\) then \({\bf x}={\bf a}\)

Fact

If \({\bf a} \ne {\bf b}\), then \(\exists \, \epsilon > 0\) such that \(B_\epsilon({\bf a}) \cap B_\epsilon({\bf b}) = \emptyset\)

Definition

A sequence \(\{{\bf x}_n\}\) in \(\mathbb{R}^K\) is a function from \(\mathbb{N}\) to \(\mathbb{R}^K\)

Definition

Sequence \(\{{\bf x}_n\}\) is said to converge to \({\bf a} \in \mathbb{R}^K\) if

\[ \forall \epsilon > 0, \; \exists \, N \in \mathbb{N} \; \text{ such that } n \geq N \implies {\bf x}_n \in B_{\epsilon}({\bf a}) \]

We say: “\(\{{\bf x}_n\}\) is eventually in any \(\epsilon\)-neighborhood of \({\bf a}\)”

In this case \({\bf a}\) is called the limit of the sequence, and we write

\[ {\bf x}_n \to {\bf a} \; \text{ as } \; n \to \infty \quad \text{or} \quad \lim_{n \to \infty} {\bf x}_n = {\bf a} \]

Definition

We call \(\{ {\bf x}_n \}\) convergent if it converges to some limit in \(\mathbb{R}^K\)

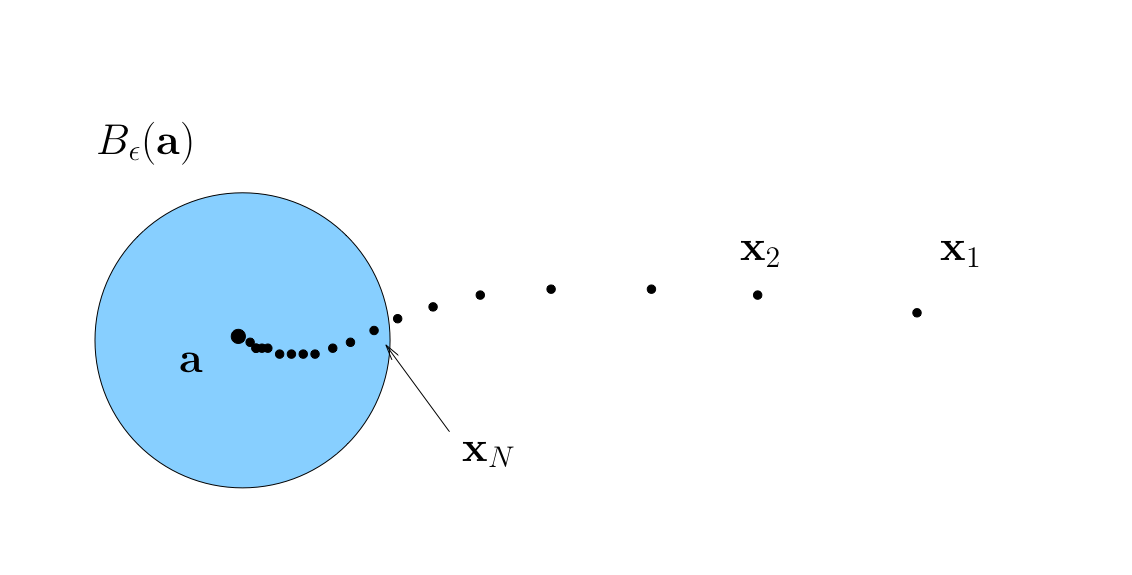
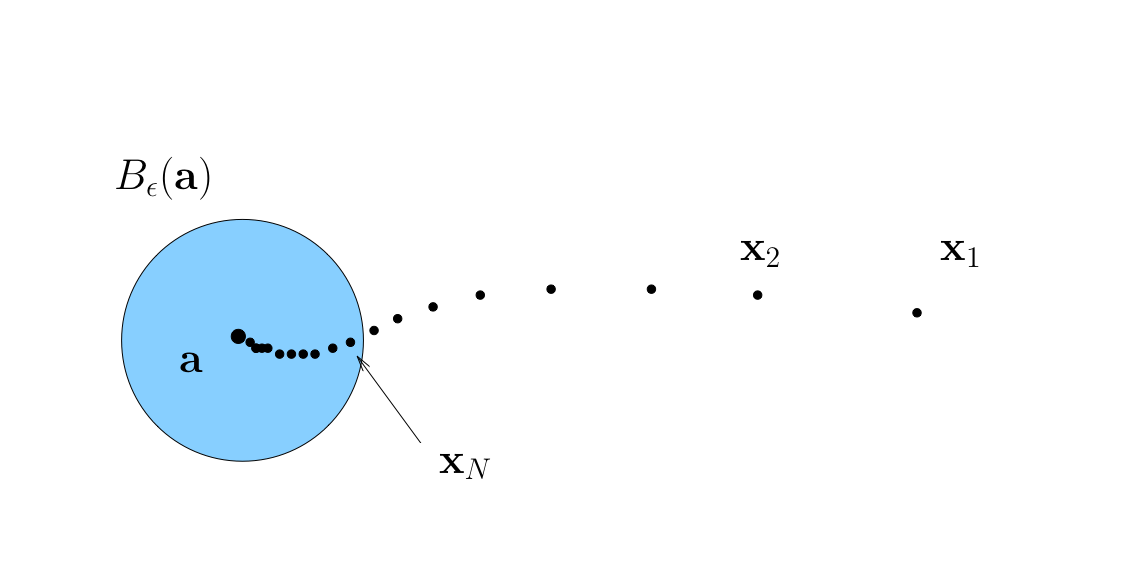
Vector vs Componentwise Convergence

Fact

A sequence \(\{{\bf x}_n\}\) in \(\mathbb{R}^K\) converges to \({\bf a} \in \mathbb{R}^K\) if and only if each component sequence converges in \(\mathbb{R}\)

That is,

\[\begin{split} \begin{pmatrix} x^1_n \\ \vdots \\ x^K_n \end{pmatrix} \to \begin{pmatrix} a^1 \\ \vdots \\ a^K \end{pmatrix} \quad \text{in } \mathbb{R}^K \quad \iff \quad \begin{array}{cc} x^1_n \to a^1 & \quad \text{in } \mathbb{R} \\ \vdots & \\ x^K_n \to a^K & \quad \text{in } \mathbb{R} \end{array} \end{split}\]

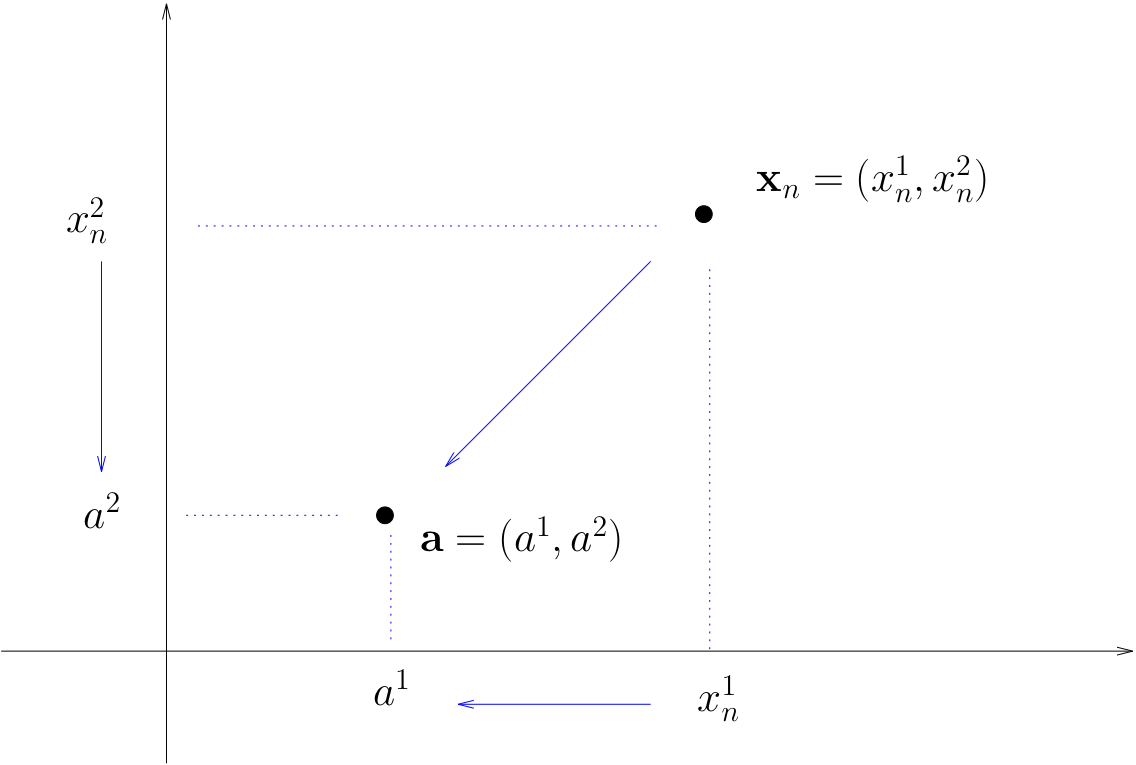
From Scalar to Vector Analysis

More definitions analogous to scalar case:

Definition

A sequence \(\{{\bf x}_n\}\) is called Cauchy if

\[ \forall \; \epsilon > 0, \;\; \exists \; N \in \mathbb{N} \; \mathrm{such\;that}\; n, m \geq N \implies \| {\bf x}_n - {\bf x}_m \| < \epsilon \]

Definition

A sequence \(\{{\bf x}_{n_k} \}\) is called a subsequence of \(\{{\bf x}_n\}\) if

1. \(\{{\bf x}_{n_k} \}\) is a subset of \(\{{\bf x}_n\}\)

2. the indices \(n_k\) are strictly increasing

Fact

Analogous to the scalar case,

1. \({\bf x}_n \to {\bf a}\) in \(\mathbb{R}^K\) if and only if \(\|{\bf x}_n - {\bf a}\| \to 0\) in \(\mathbb{R}\)

2. If \({\bf x}_n \to {\bf x}\) and \({\bf y}_n \to {\bf y}\) then \({\bf x}_n + {\bf y}_n \to {\bf x} + {\bf y}\)

3. If \({\bf x}_n \to {\bf x}\) and \(\alpha \in \mathbb{R}\) then \(\alpha {\bf x}_n \to \alpha {\bf x}\)

4. If \({\bf x}_n \to {\bf x}\) and \({\bf z} \in \mathbb{R}^K\) then \({\bf z}' {\bf x}_n \to {\bf z}' {\bf x}\)

5. Each sequence in \(\mathbb{R}^K\) has at most one limit

6. Every convergent sequence in \(\mathbb{R}^K\) is bounded

7. Every convergent sequence in \(\mathbb{R}^K\) is Cauchy

8. Every Cauchy sequence in \(\mathbb{R}^K\) is convergent

Exercise: Adapt proofs given for the scalar case to these results

Example

Let’s check that

\[ {\bf x}_n \to {\bf a} \text{ in } \mathbb{R}^K \; \iff \; \|{\bf x}_n - {\bf a}\| \to 0 \text{ in } \mathbb{R} \]

Proof

• \({\bf x}_n \to {\bf a}\) in \(\mathbb{R}^K\) means that

\[ \forall \, \epsilon > 0, \; \exists \, N \in \mathbb{N} \; \mathrm{such\;that} \; n \geq N \implies \| {\bf x}_n - {\bf a} \| < \epsilon \]

• \(\|{\bf x}_n - {\bf a}\| \to 0\) in \(\mathbb{R}\) means that

\[ \forall\, \epsilon > 0, \; \exists \, N \in \mathbb{N} \; \mathrm{such\;that} \; n \geq N \implies | \| {\bf x}_n - {\bf a} \| - 0 | < \epsilon \]

Obviously equivalent

Reminder — these facts are more general than scalar ones!

• True for any finite \(K\)

• So true for \(K = 1\)

• This recovers the corresponding scalar fact

You can forget the scalar fact if you remember the vector one

Fact

If \(\{ {\bf x}_n \}\) converges to \({\bf x}\) in \(\mathbb{R}^K\), then every subsequence of \(\{{\bf x}_n\}\) also converges to \({\bf x}\)

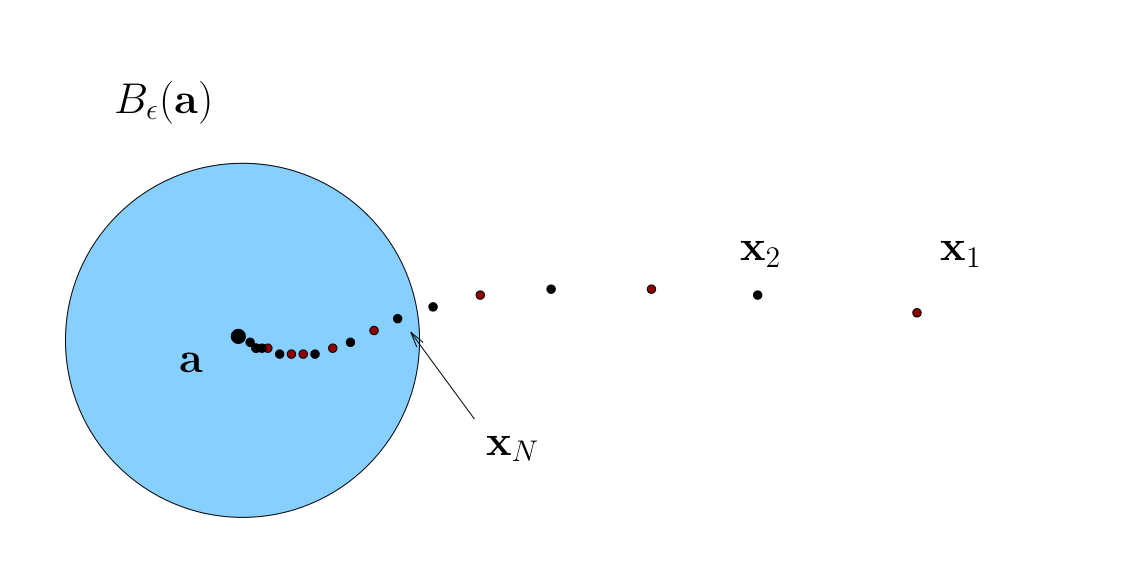
Fig. 39 Convergence of subsequences

Infinite Sums in \(\mathbb{R}^K\)

Analogous to the scalar case, an infinite sum in \(\mathbb{R}^K\) is the limit of the partial sum

Definition

If \(\{{\bf x}_n\}\) is a sequence in \(\mathbb{R}^K\), then

\[ \sum_{n=1}^{\infty} {\bf x}_n := \lim_{J\to \infty} \sum_{n=1}^J {\bf x}_n \text{ if the limit exists} \]

In other words,

\[ {\bf y} = \sum_{n=1}^{\infty} {\bf x}_n \quad \iff \quad \lim_{J \to \infty} \; \left\| \sum_{n=1}^J {\bf x}_n - {\bf y} \right\| \to 0 \]

Open and Closed Sets

Let \(G \subset \mathbb{R}^K\)

Definition

We call \({\bf x} \in G\) interior to \(G\) if \(\exists \; \epsilon > 0\) with \(B_\epsilon({\bf x}) \subset G\)

Loosely speaking, interior means “not on the boundary”

Example

If \(G = (a, b)\) for some \(a < b\), then any \(x \in (a, b)\) is interior

Proof

Fix any \(a < b\) and any \(x \in (a, b)\)

Let \(\epsilon := \min\{x - a, b - x\}\)

If \(y \in B_\epsilon(x)\) then \(y < b\) because

\[ y = y + x - x \leq |y - x| + x < \epsilon + x \leq b - x + x = b \]

Exercise: Show \(y \in B_\epsilon(x) \implies y > a\)

Example

If \(G = [-1, 1]\), then \(1\) is not interior

Intuitively, any \(\epsilon\)-ball centered on \(1\) will contain points \(> 1\)

More formally, pick any \(\epsilon > 0\) and consider \(B_\epsilon(1)\)

There exists a \(y \in B_\epsilon(1)\) such that \(y \notin [-1, 1]\)

For example, consider the point \(y := 1 + \epsilon/2\)

Exercise: Check this point: lies in \(B_\epsilon(1)\) but not in \([-1, 1]\)

Definition

A set \(G\subset \mathbb{R}^K\) is called open if all of its points are interior

Example

Open sets:

• any “open” interval \((a,b) \subset \mathbb{R}\), since we showed all points are interior

• any “open” ball \(B_\epsilon({\bf a}) = {\bf x} \in \mathbb{R}^K : \|{\bf x} - {\bf a} \| < \epsilon\)

• \(\mathbb{R}^K\) itself

Example

Sets that are not open

• \((a,b]\) because \(b\) is not interior

• \([a,b)\) because \(a\) is not interior

Closed Sets

Definition

A set \(F \subset \mathbb{R}^K\) is called closed if every convergent sequence in \(F\) converges to a point in \(F\)

Rephrased: If \(\{{\bf x}_n\} \subset F\) and \({\bf x}_n \to {\bf x}\) for some \({\bf x} \in \mathbb{R}^K\), then \({\bf x} \in F\)

Example

All of \(\mathbb{R}^K\) is closed because every sequence converging to a point in \(\mathbb{R}^K\) converges to a point in \(\mathbb{R}^K\)… right?

Example

If \((-1, 1) \subset \mathbb{R}\) is not closed

Proof

True because

1. \(x_n := 1-1/n\) is a sequence in \((-1, 1)\) converging to \(1\),

2. and yet \(1 \notin (-1, 1)\)

Example

If \(F = [a, b] \subset \mathbb{R}\) then \(F\) is closed in \(\mathbb{R}\)

Proof

Take any sequence \(\{x_n\}\) such that

• \(x_n \in F\) for all \(n\)

• \(x_n \to x\) for some \(x \in \mathbb{R}\)

We claim that \(x \in F\)

Recall that (weak) inequalities are preserved under limits:

• \(x_n \leq b\) for all \(n\) and \(x_n \to x\), so \(x \leq b\)

• \(x_n \geq a\) for all \(n\) and \(x_n \to x\), so \(x \geq a\)

therefore \(x \in [a, b] =: F\)

Example

Any “hyperplane” of the form

\[ H = \{ {\bf x} \in \mathbb{R}^K : {\bf x}' {\bf a} = c \} \]

is closed

Proof

Fix \({\bf a} \in \mathbb{R}^K\) and \(c \in \mathbb{R}\) and let \(H\) be as above

Let \(\{{\bf x}_n\} \subset H\) with \({\bf x}_n \to {\bf x} \in \mathbb{R}^K\)

We claim that \({\bf x} \in H\)

Since \({\bf x}_n \in H\) and \({\bf x}_n \to {\bf x}\) we have

\[ {\bf x}_n ' {\bf a} \to {\bf x}' {\bf a} \text{ in } \mathbb{R} \quad \text{and} \quad {\bf x}_n' {\bf a} = c \text{ for all } n \]

\[ \text{therefore } {\bf x}' {\bf a} = \lim_{n} {\bf x}_n' {\bf a} = \lim_n c = c \]

\[ \text{therefore } {\bf x} \in H \]

Properties of Open and Closed Sets

Fact

\(G \subset \mathbb{R}^K\) is open \(\iff \; G^c\) is closed

Proof

\(\implies\)

First prove necessity

Pick any \(G\) and let \(F := G^c\)

Suppose to the contrary that \(G\) is open but \(F\) is not closed, so

\(\exists\) a sequence \(\{{\bf x}_n\} \subset F\) with limit \({\bf x} \notin F\)

Then \({\bf x} \in G\), and since \(G\) open, \(\exists \, \epsilon > 0\) such that \(B_\epsilon({\bf x}) \subset G\)

Since \({\bf x}_n \to {\bf x}\) we can choose an \(N \in \mathbb{N}\) with \({\bf x}_N \in B_\epsilon({\bf x})\)

This contradicts \({\bf x}_n \in F\) for all \(n\)

\(\Longleftarrow\)

Next prove sufficiency

Pick any closed \(F\) and let \(G := F^c\), need to prove that \(G\) is open

Suppose to the contrary that \(G\) is not open

Then exists some non-interior \({\bf x} \in G\), that is no \(\epsilon\)-ball around \(x\) lies entirely in \(G\)

Then it is possible to find a sequence \(\{{\bf x}_n\}\) which converges to \(x \in G\), but every element of which lies in the \(B_{1/n}({\bf x}) \cap F\)

This contradicts the fact that \(F\) is closed

Example

Any singleton \(\{ {\bf x} \} \subset \mathbb{R}^K\) is closed

Proof

Let’s prove this by showing that \(\{{\bf x}\}^c\) is open

Pick any \({\bf y} \in \{{\bf x}\}^c\)

We claim that \({\bf y}\) is interior to \(\{{\bf x}\}^c\)

Since \({\bf y} \in \{{\bf x}\}^c\) it must be that \({\bf y} \ne {\bf x}\)

Therefore, exists \(\epsilon > 0\) such that \(B_\epsilon({\bf y}) \cap B_\epsilon({\bf x}) = \emptyset\)

In particular, \({\bf x} \notin B_\epsilon({\bf y})\), and hence \(B_\epsilon({\bf y}) \subset \{{\bf x}\}^c\)

Therefore \({\bf y}\) is interior as claimed

Since \({\bf y}\) was arbitrary it follows that \(\{{\bf x}\}^c\) is open and \(\{{\bf x}\}\) is closed

Fact

1. Any union of open sets is open

2. Any intersection of closed sets is closed

Proof

Proof of first fact:

Let \(G := \cup_{\lambda \in \Lambda} G_\lambda\), where each \(G_\lambda\) is open

We claim that any given \({\bf x} \in G\) is interior to \(G\)

Pick any \({\bf x} \in G\)

By definition, \({\bf x} \in G_\lambda\) for some \(\lambda\)

Since \(G_\lambda\) is open, \(\exists \, \epsilon > 0\) such that \(B_\epsilon({\bf x}) \subset G_\lambda\)

But \(G_\lambda \subset G\), so \(B_\epsilon({\bf x}) \subset G\) also holds

In other words, \({\bf x}\) is interior to \(G\)

But be careful:

• An infinite intersection of open sets is not necessarily open

• An infinite union of closed sets is not necessarily closed

For example, if \(G_n := (-1/n, 1/n)\), then \(\cap_{n \in \mathbb{N}} G_n = \{0\} \)

To see this, suppose that \(x \in \cap_n G_n\)

Then

\[ -1/n < x < 1/n, \quad \forall n \in \mathbb{N} \]

Therefore \(x = 0\), and hence \(x \in \{0\}\)

On the other hand, if \(x \in \{0\}\) then \(x \in \cap_n G_n\)

Fact

If \(A\) is closed and bounded then every sequence in \(A\) has a subsequence which converges to a point of \(A\)

Take any sequence \(\{{\bf x}_n\}\) contained in \(A\)

Since \(A\) is bounded, \(\{{\bf x}_n\}\) is bounded

Therefore it has a convergent subsequence

Since the subsequence is also contained in \(A\), and \(A\) is closed, the limit must lie in \(A\).

Definition

Bounded and closed sets are called compact sets or compacts

Continuity

One of the most fundamental properties of functions

Related to existence of

• optima

• roots

• fixed points

• etc

as well as a variety of other useful concepts

Definition

A function \(F\) is called bounded if its range is a bounded set.

Fact

If \(F\) and \(G\) are bounded, then so are \(F+G\), \(F \cdot G\) and \(\alpha F\) for any finite \(\alpha\)

Proof

Proof for the case \(F + G\):

Let \(F\) and \(G\) be bounded functions

\(\exists\) \(M_F\) and \(M_G\) s.t. \(\| F({\bf x}) \| \leq M_F\) and \(\| G({\bf x}) \| \leq M_G\) for all \({\bf x}\)

Fix any \({\bf x}\) and let \(M := M_F + M_G\)

Applying the triangle inequality gives

\[ \| (F + G)({\bf x}) \| := \| F({\bf x}) + G({\bf x}) \| \leq \| F({\bf x}) \| + \| G({\bf x}) \| \leq M \]

Since \({\bf x}\) was arbitrary this bound holds for all \({\bf x}\)

Let \(F \colon A \to \mathbb{R}^J\) where \(A\) is a subset of \(\mathbb{R}^K\)

Definition

\(F\) is called continuous at \({\bf x} \in A\) if as \(n \to \infty\)

\[ {\bf x}_n \to {\bf x} \quad \implies \quad F({\bf x}_n) \to F({\bf x}) \]

Requires that

• \(F({\bf x}_n)\) converges for each choice of \({\bf x}_n \to {\bf x}\),

• The limit is always the same, and that limit is \(F({\bf x})\)

Definition

\(F\) is called continuous if it is continuous at every \({\bf x} \in A\)

Fig. 40 Continuity

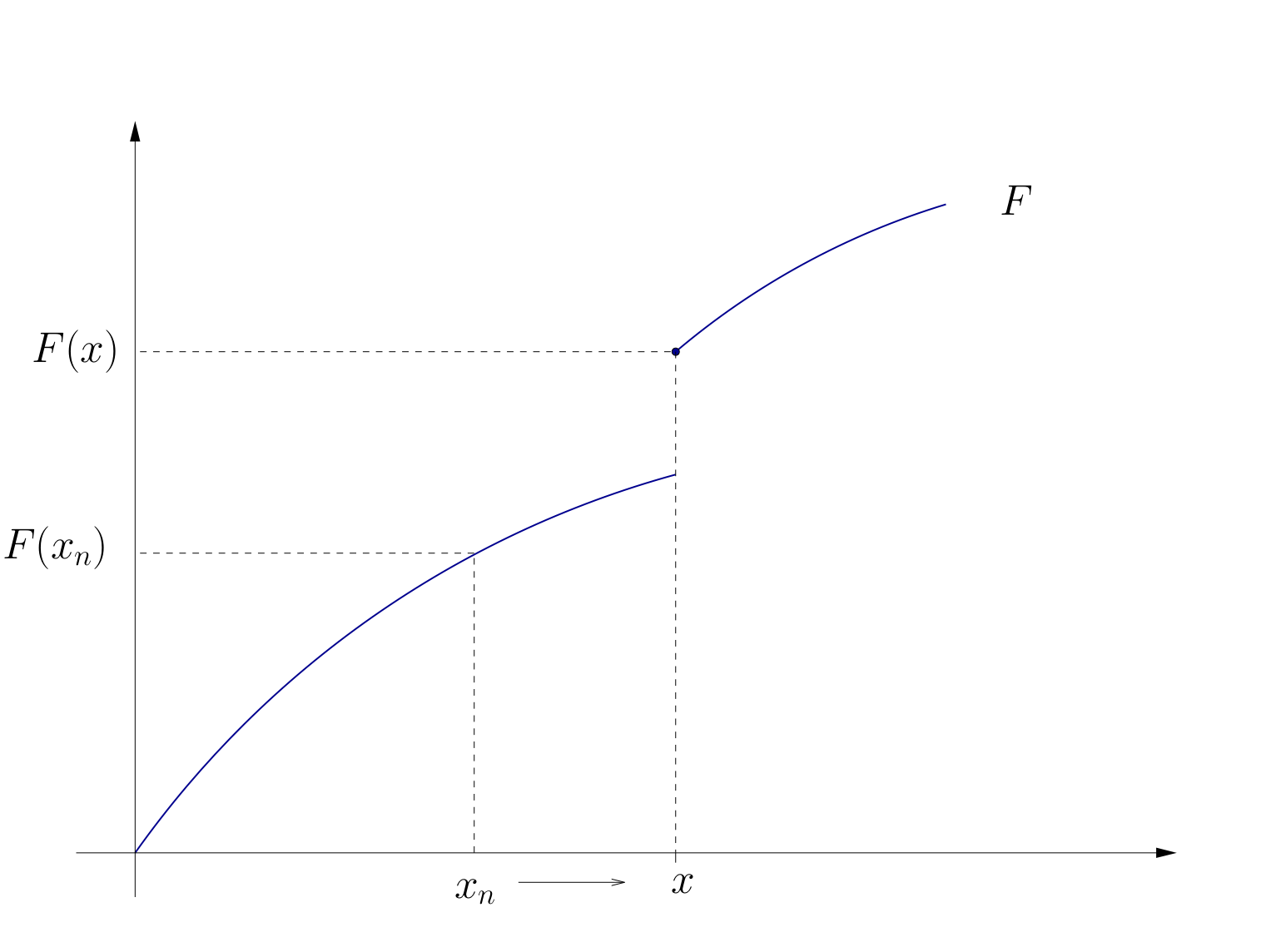
Fig. 41 Discontinuity at \(x\)

Example

Let \({\bf A}\) be an \(J \times K\) matrix and let \(F({\bf x}) = {\bf A} {\bf x}\)

The function \(F\) is continuous at every \({\bf x} \in \mathbb{R}^K\)

To see this take

• any \({\bf x} \in \mathbb{R}^K\)

• any \({\bf x}_n \to {\bf x}\)

By the definition of the matrix norm \(\| {\bf A} \|\), we have

\[ \| {\bf A} {\bf x}_n - {\bf A} {\bf x} \| = \| {\bf A} ({\bf x}_n - {\bf x}) \| \leq \| {\bf A} \| \| {\bf x}_n - {\bf x} \| \]

\[ \text{therefore } {\bf x}_n \to {\bf x} \implies {\bf A} {\bf x}_n \to {\bf A} {\bf x} \]

Exercise: Exactly what rules are we using here?

Fact

If \(f \colon \mathbb{R} \to \mathbb{R}\) is differentiable at \(x\), then \(f\) is continuous at \(x\)

Fact

Some functions known to be continuous on their domains:

• \(x \mapsto x^\alpha\)

• \(x \mapsto |x|\)

• \(x \mapsto \log(x)\)

• \(x \mapsto \exp(x)\)

• \(x \mapsto \sin(x)\)

• \(x \mapsto \cos(x)\)

Example

Discontinuous at zero: \(x \mapsto \mathbb{1}\{x > 0\}\).

Fact

Let \(F\) and \(G\) be functions and let \(\alpha \in \mathbb{R}\)

1. If \(F\) and \(G\) are continuous at \({\bf x}\) then so is \(F + G\), where

\[ (F + G)({\bf x}) := F({\bf x}) + G({\bf x}) \]

2. If \(F\) is continuous at \({\bf x}\) then so is \(\alpha F\), where

\[ (\alpha F)({\bf x}) := \alpha F({\bf x}) \]

3. If \(F\) and \(G\) are continuous at \({\bf x}\) and real valued then so is \(FG\), where

\[ (FG)({\bf x}) := F({\bf x}) \cdot G({\bf x}) \]

In the latter case, if in addition \(G({\bf x}) \ne 0\), then \(F/G\) is also continuous.

As a result, set of continuous functions is “closed” under elementary arithmetic operations

Example

The function \(F \colon \mathbb{R} \to \mathbb{R}\) defined by

\[ F(x) = \frac{\exp(x) + \sin(x)}{2 + \cos(x)} + \frac{x^4}{2} - \frac{\cos^3(x)}{8!} \]

is continuous

Proof

Just repeatedly apply the rules on the previous slide

Let’s just check that

\[ \text{$F$ and $G$ continuous at ${\bf x}$} \implies \text{$F + G$ continuous at ${\bf x}$} \]

Let \(F\) and \(G\) be continuous at \({\bf x}\)

Pick any \({\bf x}_n \to {\bf x}\)

We claim that \(F({\bf x}_n) + G({\bf x}_n) \to F({\bf x}) + G({\bf x})\)

By assumption, \(F({\bf x}_n) \to F({\bf x})\) and \(G({\bf x}_n) \to G({\bf x})\)

From this and the triangle inequality we get

\[ \| F({\bf x}_n) + G({\bf x}_n) - (F({\bf x}) + G({\bf x})) \| \leq \]

\[ \leq \| F({\bf x}_n) - F({\bf x}) \| + \| G({\bf x}_n) - G({\bf x}) \| \to 0 \]

Extra material

Watch excellent video by Grant Sanderson (3blue1brown) on limits, and continue onto his whole amazing series on calculus