Elements of set theory

Elements of set theory#

ECON2125/6012 Lecture 3
Fedor Iskhakov

Announcements & Reminders

None

Plan for this lecture

We now turn to more formal / foundational ideas

Logic and proofs
Sets, operations with sets
Sequences, limits, operations with limits
Functions, properties of functions
Differentiation, Taylor series
+
Analysis in $\mathbb{R}^n$

Mainly review of key ideas

Supplementary reading:

Simon & Blume: Appendix A1.1, A1.2, A1.3
Sundaram: Appendix A

Common symbols

$P \implies Q$ means “$P$ implies $Q$”
$P \iff Q$ means “$P \implies Q$ and $Q \implies P$”
$\exists$ means “there exists”
$\forall$ means “for all”
s.t. means “such that”
$\because$ means “because” (not used very often)
$\therefore$ means “therefore” (not used very often)
$a := 1$ means “$a$ is defined to be equal to 1” (alternatively $a \equiv 1$ or $a \stackrel{def.}{=} 1 $)
$\mathbb{R}$ means all real numbers
$\mathbb{N}$ means the natural numbers $\{1, 2, \ldots \}$
$\mathbb{Z}$ means integers $\{\ldots, -2,-1,0,1, 2, \ldots \}$
$\mathbb{Q}$ means the rational numbers (ratios of two integers)

Logic#

Let $P$ and $Q$ be statements, such as

$x$ is a negative integer
$x$ is an odd number
the area of any circle in the plane is $-2 \pi R$

Fact

Law of the excluded middle: Every mathematical statement is either true or false

Statement “$P \implies Q$” means “$P$ implies $Q$”

Example

$k$ is even $\implies$ $k = 2n$ for some integer $n$

Equivalent forms of $P \implies Q$:

If $P$ is true then $Q$ is true
$P$ is a sufficient condition for $Q$
$Q$ is a necessary condition for $P$
If $Q$ fails then $P$ fails

Equivalent ways of saying $P \nRightarrow Q$ (does not imply):

$P$ does not imply $Q$
$P$ is not sufficient for $Q$
$Q$ is not necessary for $P$
Even if $Q$ fails, $P$ can still hold

Example

Let

$P := $ “$n \in \mathbb{N}$ and even”
$Q := $ “$n$ even”

Then

$P \implies Q$
$P$ is sufficient for $Q$
$Q$ is necessary for $P$
If $Q$ fails then $P$ fails

Example

Let

$P := $ “$R$ is a rectangle”
$Q := $ “$R$ is a square”

Then

$P \not \Rightarrow Q$
$P$ is not sufficient for $Q$
$Q$ is not necessary for $P$
Just because $Q$ fails does not mean that $P$ fails

Proof by contradiction#

Suppose we wish to prove a statement such as $P \implies Q$

A proof by contradiction starts by assuming the opposite: $P$ holds and yet $Q$ fails.
We then show that this scenario leads to a contradiction

Examples of contradictions

$1 < 0$
$10$ is an odd number

We then conclude that $P \implies Q$ is valid after all.

Example: proof by contradiction

Suppose that island X is populated only by pirates and knights:

pirates always lie
knights always tell the truth

Claim to prove: If person Y says "I'm a pirate" then person Y is not a native of island X

Strategy for the Proof:

Suppose person Y is a native of the island
Show that this leads to a contradiction
Conclude that Y is not a native of island X, as claimed

Example

There is no $x \in \mathbb{R}$ such that $0 < x < 1/n$, $\forall n \in \mathbb{N}$.

Example

Let $n \in \mathbb{N}$. Show that $n^2$ odd $\implies$ $n$ odd

Sets#

Will often refer to the real numbers, $\mathbb{R}$

Understand it to contain “all of the numbers” on the “real line”

Contains both the rational and the irrational numbers

$\mathbb{R}$ is an example of a set

A set is a collection of objects viewed as a whole

(In case of $\mathbb{R}$, the objects are numbers)

Other examples of sets:

set of all rectangles in the plane
set of all prime numbers
set of students in the class

Notation:

Sets: $A, B, C$
Elements: $x,y,z$

Important sets:

$\mathbb{N} := \{1, 2, 3, \ldots \}$
$\mathbb{Z} := \{\ldots, -2, -1, 0, 1, 2, \ldots \}$
$\mathbb{Q} := \{ p/q : p, q \in \mathbb{Z}, \; q \ne 0 \}$
$\mathbb{R} := \mathbb{Q} \cup \{ \text{ irrationals } \}$

Definition of a set

A set $A$ can be defined by either

direct enumeration of its elements
defining a formula for infinite number of elements
as a subset of already defined set $B$ and known function $\psi(x)$

\[ A = \{ \psi(x), x \in B \colon \text{condition on x}\} \]

Intervals of $\mathbb{R}$#

Common notation:

\[ (a, b) := \{ x \in \mathbb{R} : a < x < b \} \]

\[ (a, b] := \{ x \in \mathbb{R} : a < x \leq b \} \]

\[ [a, b) := \{ x \in \mathbb{R} : a \leq x < b \} \]

\[ [a, b] := \{ x \in \mathbb{R} : a \leq x \leq b \} \]

\[ [a, \infty) := \{ x \in \mathbb{R} : a \leq x \} \]

\[ (-\infty, b) := \{ x \in \mathbb{R} : x < b \} \]

Etc.

Operations with sets#

Let $A$ and $B$ be any sets

Statement $x \in A$ means that $x$ is an element of $A$

$A \subset B$ means that any element of $A$ is also an element of $B$

Example

$\mathbb{N} \subset \mathbb{Z}$
irrational numbers are a subset of $\mathbb{R}$

Equality of $A$ and $B$

Let $S$ be any set and $A$ and $B$ be subsets of $S$

$A = B$ means that $A$ and $B$ contain the same elements

Equivalently, $A = B$ $\iff$ $A \subset B$ and $B \subset A$

Definition

Union of $A$ and $B$

\[ A \cup B := \{ x \in S : x \in A \text{ or } x \in B \} \]

Intersection of $A$ and $B$

\[ A \cap B := \{ x \in S : x \in A \text{ and } x \in B \} \]

Set theoretic difference of $A$ and $B$

\[ A \setminus B := \{ x \in S : x \in A \text{ and } x \notin B \} \]

In other words, all points in $A$ that are not points in $B$

Example

$\mathbb{Z} \setminus \mathbb{N} = \{\ldots, -2, -1, 0\}$
$\mathbb{R} \setminus \mathbb{Q} = $ the set of irrational numbers
$\mathbb{R} \setminus [0, \infty) = (-\infty, 0)$
$\mathbb{R} \setminus (a, b) = (-\infty, a] \cup [b, \infty)$

Definition

Complement of $A$

All elements of $S$ that are not in $A$:

\[ A^c := S \setminus A :=: \{ x \in S : x \notin A \} \]

Remarks:

Need to know what $S$ is before we can determine $A^c$
If not clear better write $S \setminus A$

Example

$(a,\infty)^c$ generally understood to be $(-\infty, a]$

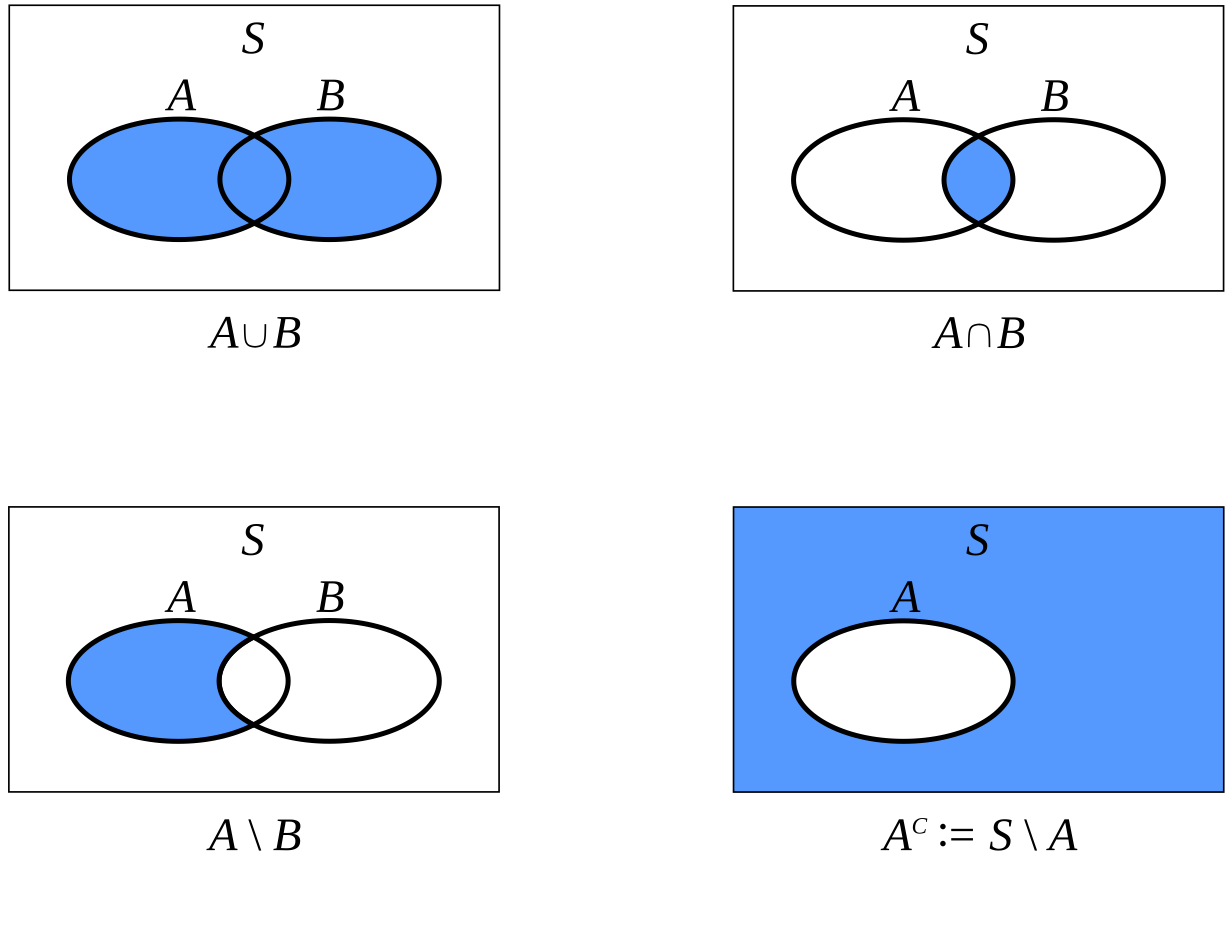
_images/allsets.png — Fig. 21 \label{f:allsets} Unions, intersections and complements#

Set operations properties#

If $A$ and $B$ subsets of $S$, then

$A \cup B = B \cup A$ and $A \cap B = B \cap A$

$(A \cup B)^c = B^c \cap A^c$ and $(A \cap B)^c = B^c \cup A^c$
$A \setminus B = A \cap B^c$

$(A^c)^c = A$

The empty set $\emptyset$ is the set containing no elements

If $A \cap B = \emptyset$, then $A$ and $B$ said to be disjoint

Infinite Unions and Intersections#

Given a family of sets $K_{\lambda} \subset S$ with $\lambda \in \Lambda$,

\[ \bigcap_{\lambda \in \Lambda} K_{\lambda} := \{ x \in S : x\in K_{\lambda} \textnormal{ for all } \lambda \in \Lambda \} \]

\[ \bigcup_{\lambda \in \Lambda} K_{\lambda} := \{x \in S \colon \textnormal{there exists an } \lambda \in \Lambda \textnormal{ such that } x\in K_{\lambda} \} \]

“there exists” means “there exists at least one”

Example

Let $A := \cap_{n \in \mathbb{N}} (0, 1/n)$

Claim: $A = \emptyset$

Proof

We need to show that $A$ contains no elements

Suppose to the contrary that $x \in A = \cap_{n \in \mathbb{N}} (0, 1/n)$

Then $x$ is a number satisfying $0 < x < 1/n$ for all $n \in \mathbb{N}$

No such $x$ exists as we showed above. Contradiction.

Example

For any $a < b$ we have $\cup_{\epsilon > 0 } \; [a + \epsilon, b) = (a, b)$

Proof

To show equality of the sets, we show that RHS $\subset$ LHS and LHS $\subset$ RHS

Pick any $a < b$

Suppose first that $x \in \cup_{\epsilon > 0 } \; [a + \epsilon, b)$

This means there exists $\epsilon > 0$ such that $a + \epsilon \leq x < b$

Clearly $a < x < b$, and hence $x \in (a, b)$

Conversely, if $a < x < b$, then $\exists \, \epsilon > 0$ s.t. $a + \epsilon \leq x < b$

Hence $x \in \cup_{\epsilon > 0 } \; [a + \epsilon, b)$

Fact: de Morgan’s laws

Let $S$ be any set and let $K_{\lambda} \subset S$ for all $\lambda \in \Lambda$. Then

\[ \left[ \bigcup_{\lambda \in \Lambda} K_{\lambda} \right]^{c} = \bigcap_{\lambda \in \Lambda} K_{\lambda}^{c} \quad \text{and} \quad \left[ \bigcap_{\lambda \in \Lambda} K_{\lambda} \right]^{c} = \bigcup_{\lambda \in \Lambda} K_{\lambda}^{c} \]

Let’s prove that $A := \left( \cup_{\lambda \in \Lambda} K_{\lambda} \right)^{c} = \cap_{\lambda \in \Lambda} K_{\lambda}^{c} =: B$

Suffices to show that $A \subset B$ and $B \subset A$

Let’s just do $A \subset B$

Must show that every $x \in A$ is also in $B$

Fix $x \in A$

Since $x \in A$, it must be that $x$ is not in $\cup_{\lambda \in \Lambda} K_{\lambda}$

\[ \text{therefore } \text{ $x$ is not in any $K_{\lambda}$ } \]

\[ \text{therefore } x \in K_{\lambda}^c \text{ for each } \lambda \in \Lambda \]

\[ \text{therefore } x \in \cap_{\lambda \in \Lambda} K_{\lambda}^{c} =: B \]

Tuples#

We often organize collections with natural order into “tuples”

Definition

A tuple is

a finite ordered sequence of terms
denoted using notation such as $(a_1, a_2)$ or $(x_1, x_2, x_3)$

Example

Flip a coin 10 times and let

$0$ represent tails and $1$ represent heads

Typical outcome $(1, 1, 0, 0, 0, 0, 1, 0, 1, 1)$

Generic outcome $(b_1, b_2, \ldots, b_{10})$ for $b_n \in \{0, 1\}$

Cartesian Products#

We make collections of tuples using Cartesian products

Definition

The Cartesian product of $A_1, \ldots, A_N$ is the set

\[ A_1 \times \cdots \times A_N := \{ (a_1, \ldots, a_N) : a_n \in A_n \text{ for } n =1, \ldots, N \} \]

Example

\[ ```[0, 8] \times [0, 1] = \{ (x_1,x_2) : 0 \leq x_1 \leq 8, \, 0 \leq x_2 \leq 1 \} \]

Example

Set of all outcomes from flip experiment is

\[ B := \Big\{ (b_1, \ldots, b_{10}) : b_n \in \{0, 1\} \text{ for } n = 1, \ldots, 10 \Big\} \]

\[ = \{0, 1\} \times \cdots \times \{0, 1\} \quad (10 \text{ products}) \]

Example

The vector space $\mathbb{R}^N$ is the Cartesian product

\[ \mathbb{R}^N = \mathbb{R} \times \cdots \times \mathbb{R} \quad (N \text{ times}) \]

\[ = \{ \, \text{all tuples } (x_1, \ldots, x_N) \text{ with } x_n \in \mathbb{R} \} \]

Counting Finite Sequences#

Counting methods answer common questions such as

How many arrangements of a sequence?
How many subsets of a set?

They also address deeper problems such as

How “large” is a given set?
Can we compare size of sets even when they are infinite?

The key rule is: multiply possibilities

Example

Can travel from Sydney to Tokyo in 3 ways and Tokyo to NYC in 8 ways $\implies$ can travel from Sydney to NYC in 24 ways

Example

Number of 10 letter passwords from the lowercase letters a,b,...,z is

\[ 26^{10} = 141,167,095,653,376 \]

Example

Number of possible distinct outcomes $(i, j)$ from 2 rolls of a dice is

\[ 6 \times 6 = 36 \]

Counting Cartesian Products#

Fact

If $A_n$ are finite for $n=1, \ldots,N$, then

\[ \#(A_1 \times \cdots \times A_N) = (\# A_1) \times \cdots \times (\# A_N) \]

That is, number of possible tuples $=$ product of the number of possibilities for each element

Example

Number of binary sequences of length $10$ is

\[ \# [\{0, 1\} \times \cdots \times \{0, 1\}] = 2 \times \cdots \times 2 = 2^{10} \]

Infinite Cartesian Products

If $\{A_n\}$ is a collection of sets, one for each $n \in \mathbb{N}$, then

\[ A_1 \times A_2 \times \cdots := \{ (a_1, a_2, \ldots) : a_n \in A_n \text{ for each } n \in \mathbb{N} \} \]

Sometimes denoted $\times_{n=1}^{\infty} A_n$

If $A_n = A$ for all $n$, then $\times_{n=1}^{\infty} A$ also written as $A^{\mathbb{N}}$

Example

The set of all binary sequences $\{0, 1\}^{\mathbb{N}}$

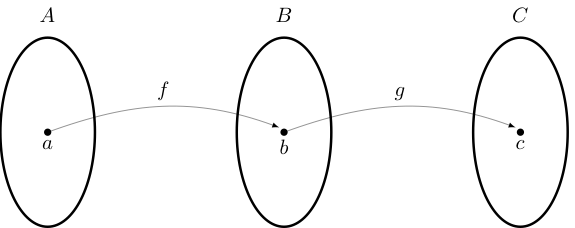
Functions#

Definition

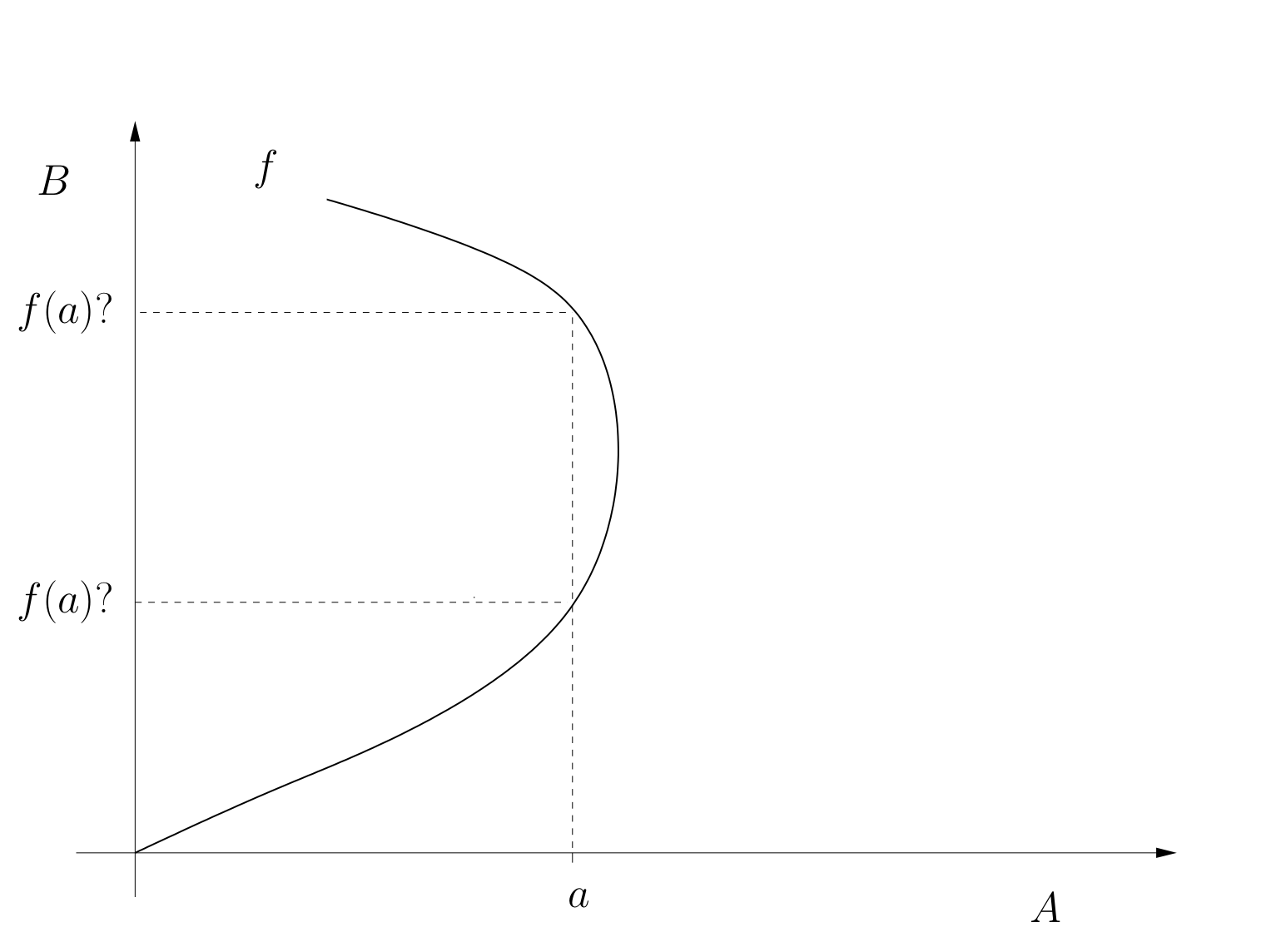
A function $f \colon A \rightarrow B$ from set $A$ to set $B$ is a rule that associates to each element of $A$ a uniquely determined element of $B$

$f \colon A \to B$ means that $f$ is a function from $A$ to $B$

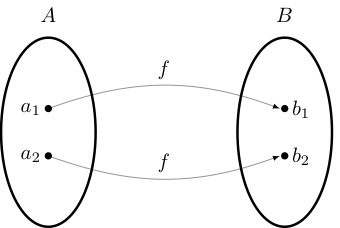
$A$ is called the domain of $f$ and $B$ is called the codomain

Example

$f$ defined by

\[ f(x) = \exp(-x^2) \]

is a function from $\mathbb{R}$ to $\mathbb{R}$

Sometimes we write the whole thing like this

\[\begin{split} f \colon \mathbb{R} \to \mathbb{R} \\ x \mapsto \exp(-x^2), \text{ or}\\ f \colon \mathbb{R} \ni x \mapsto \exp(-x^2) \in \mathbb{R} \end{split}\]

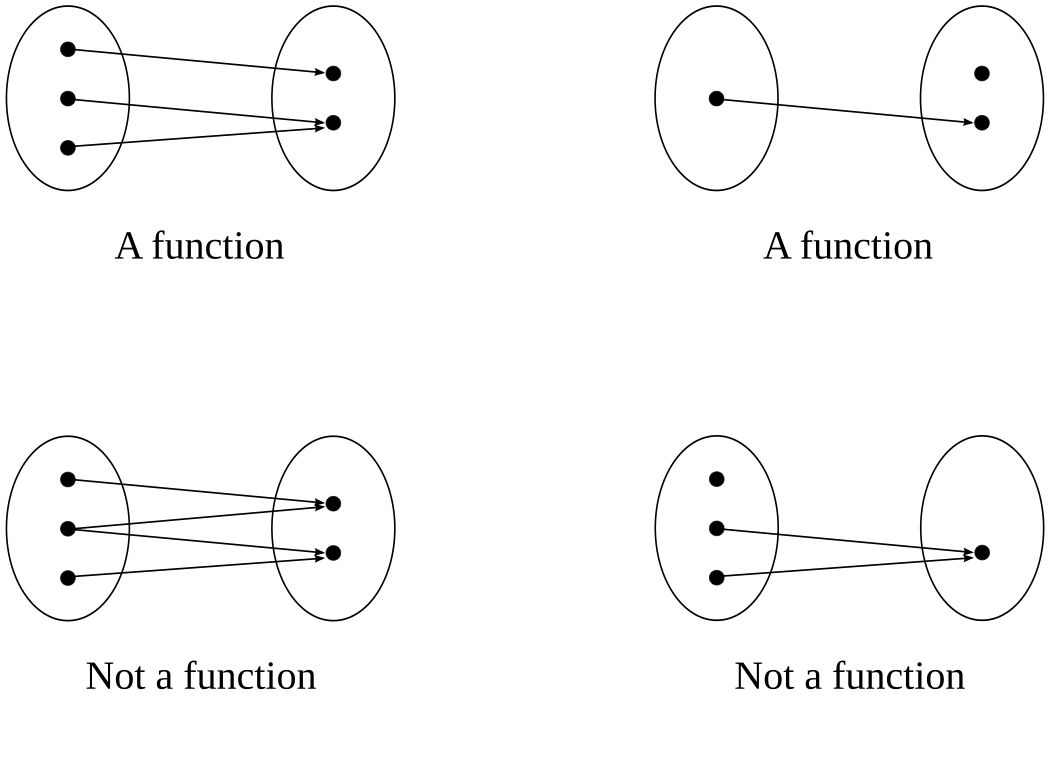
Lower panel: functions have to map all elements in domain to a uniquely determined element in codomain.

Example: not a function

Definition

For each $a \in A$, $f(a) \in B$ is called the image of $a$ under $f$

If $f(a) = b$ then $a$ is called a preimage of $b$ under $f$

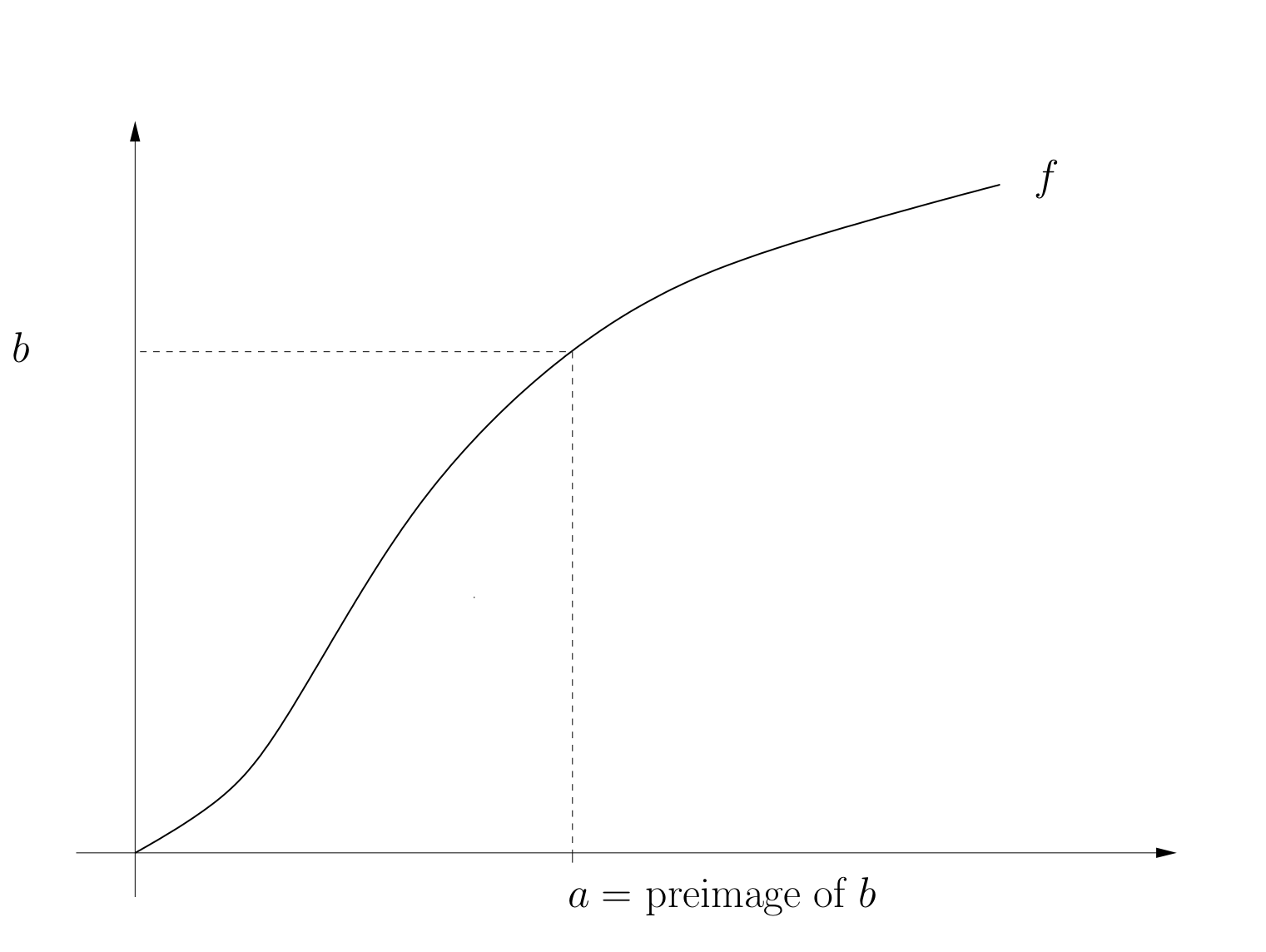
A point in $B$ can have one, many or zero preimages

The codomain of a function is not uniquely pinned down

Example

Consider the mapping defined by $f(x) = \exp(-x^2)$

Both of these statements are valid:

$f$ a function from $\mathbb{R}$ to $\mathbb{R}$
$f$ a function from $\mathbb{R}$ to $(0, \infty)$

Definition

The smallest possible codomain is called the range of $f \colon A \to B$:

\[ \mathrm{rng}(f) := \{ b \in B : f(a) = b \text{ for some } a \in A \} \]

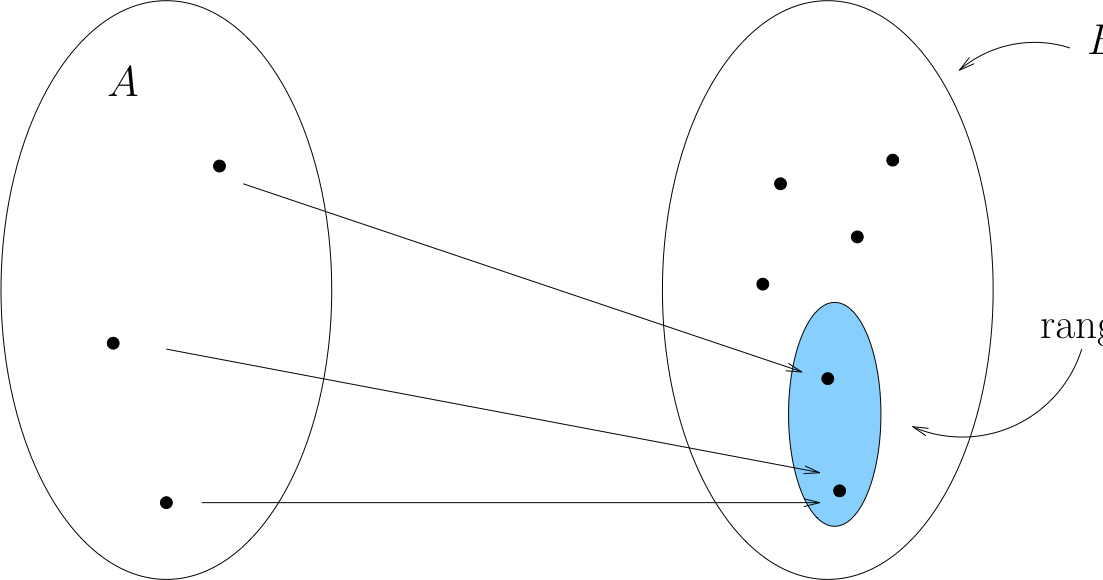
Example

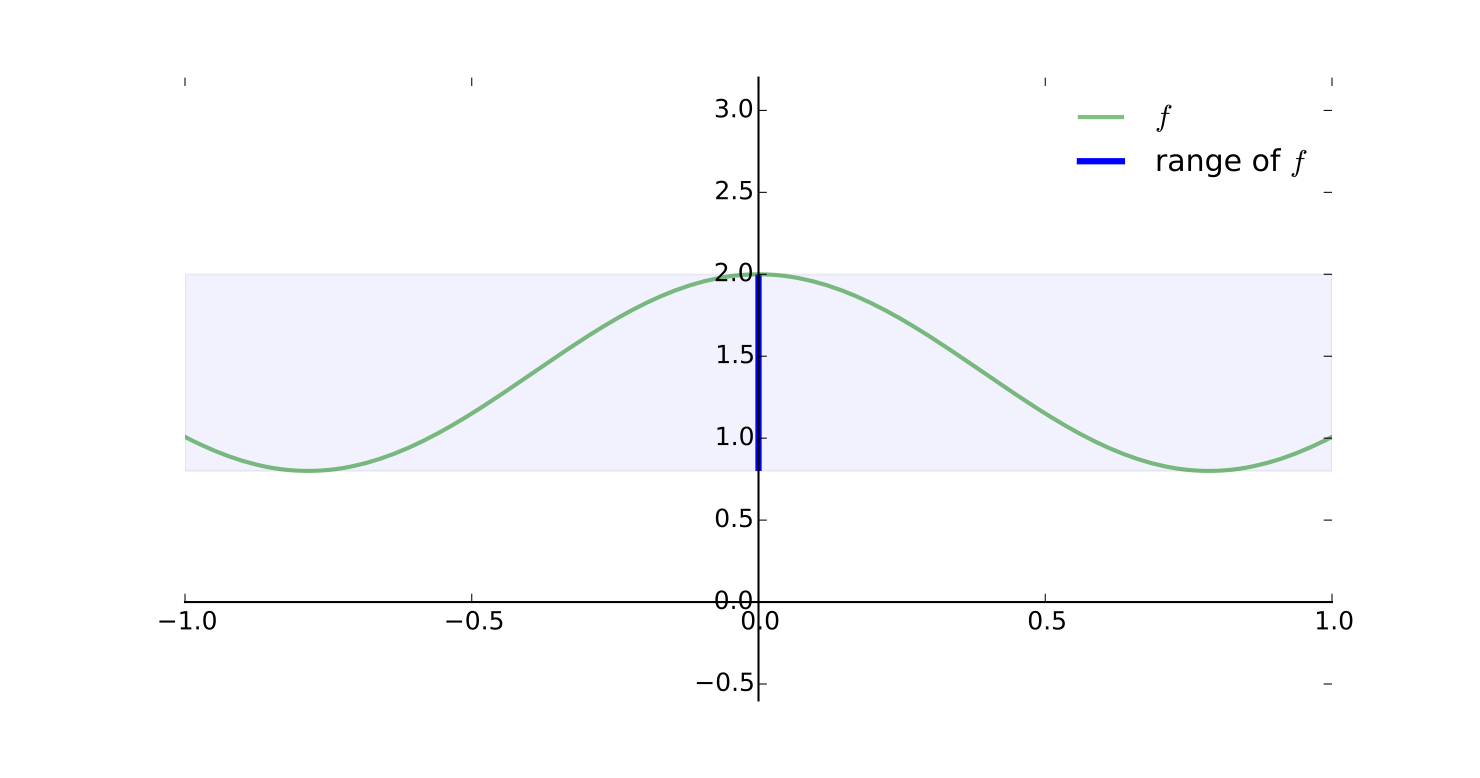
Let $f \colon [-1, 1] \to \mathbb{R}$ be defined by

\[ f(x) = 0.6 \cos(4 x) + 1.4 \]

Then $\mathrm{rng}(f) = [0.8, 2.0]$

Example

If $ f \colon [0, 1] \to \mathbb{R}$ is defined by

\[ f(x) = 2x \]

then $\mathrm{rng}(f) = [0, 2]$

Example

If $f \colon \mathbb{R} \to \mathbb{R}$ is defined by

\[ f(x) = \exp(x) \]

then $\mathrm{rng}(f) = (0, \infty)$

Proof

The composition of $f \colon A \to B$ and $g \colon B \to C$ is the function $g \circ f$ from $A$ to $C$ defined by

\[ (g \circ f)(a) = g(f(a)) \quad (a \in A) \]

Onto Functions (Surjections)#

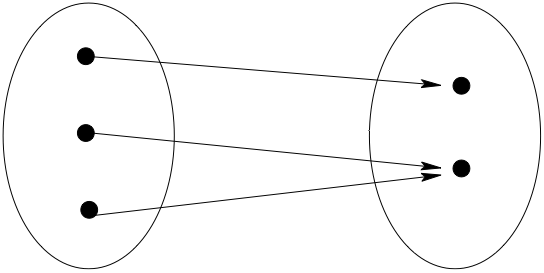
Definition

A function $f \colon A \to B$ is called onto (or surjection) if every element of $B$ is the image under $f$ of at least one point in $A$.

Equivalently, $\mathrm{rng}(f) = B$

Fact

$f \colon A \to B$ is onto if and only if each element of $B$ has at least one preimage under $f$

_images/bijection3.png — Fig. 22 Onto (surjection)#

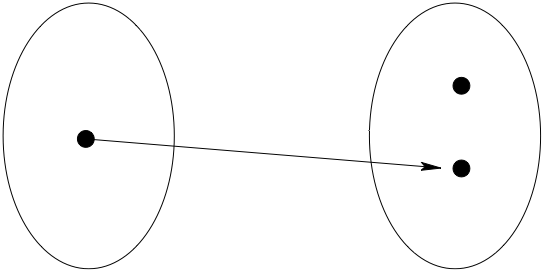
_images/function3.png — Fig. 23 Not *onto*!#

_images/bijection2.png — Fig. 24 Not *onto*!#

Example

The function $f \colon \mathbb{R} \to \mathbb{R}$ defined by

\[ f(x) = ax^3 + b x^2 + cx + d \]

is onto whenever $a \ne 0$

To see this pick any $y \in \mathbb{R}$

We claim $\exists \; x \in \mathbb{R}$ such that $f(x) = y$

Equivalent:

\[ \exists \; x \in \mathbb{R} \; \mathrm{s.t.} \; ax^3 + b x^2 + cx + d - y = 0 \]

Fact

Every cubic equation with $a \ne 0$ has at least one real root

_images/cubic.png — Fig. 25 Cubic functions from $\mathbb{R}$ to $\mathbb{R}$ are always onto#

One-to-One Functions (Injections)#

Definition

A function $f \colon A \to B$ is called one-to-one (or injection) if distinct elements of $A$ are always mapped into distinct elements of $B$.

That is, $f$ is one-to-one if

\[ a \in A, \; a' \in A \text{ and } a \ne a' \implies f(a) \ne f(a') \]

Equivalently,

\[ f(a) = f(a') \implies a = a' \]

Fact

$f \colon A \to B$ is one-to-one if and only if each element of $B$ has at most one preimage under $f$

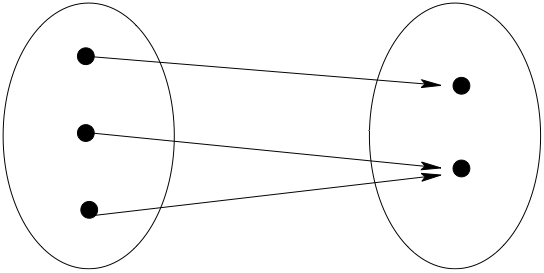
_images/bijection1.png — Fig. 28 Not one-to-one#

Bijections#

Definition

A function that is

one-to-one (injection) and
onto (surjection)

is called a bijection or one-to-one correspondence

Fact

$f \colon A \to B$ is a bijection if and only if each $b \in B$ has one and only one preimage in $A$

Example

$x \mapsto 2x$ is a bijection from $\mathbb{R}$ to $\mathbb{R}$

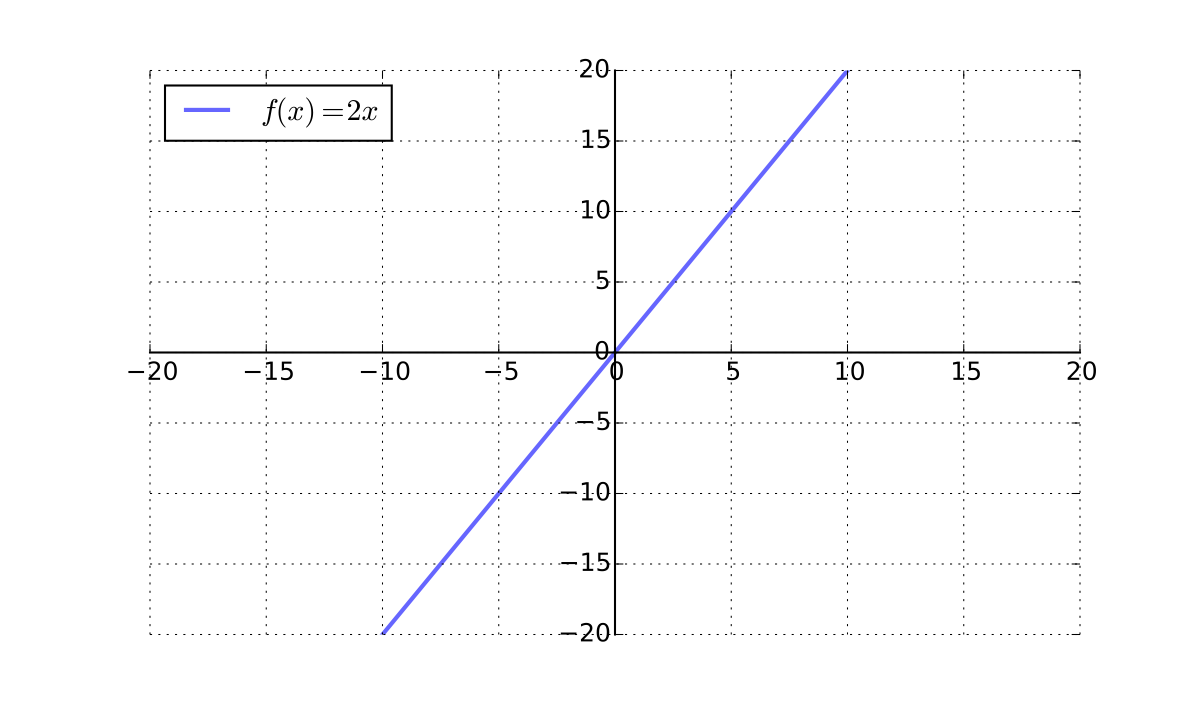
Example

$k \mapsto -k$ is a bijection from $\mathbb{Z}$ to $\mathbb{Z}$

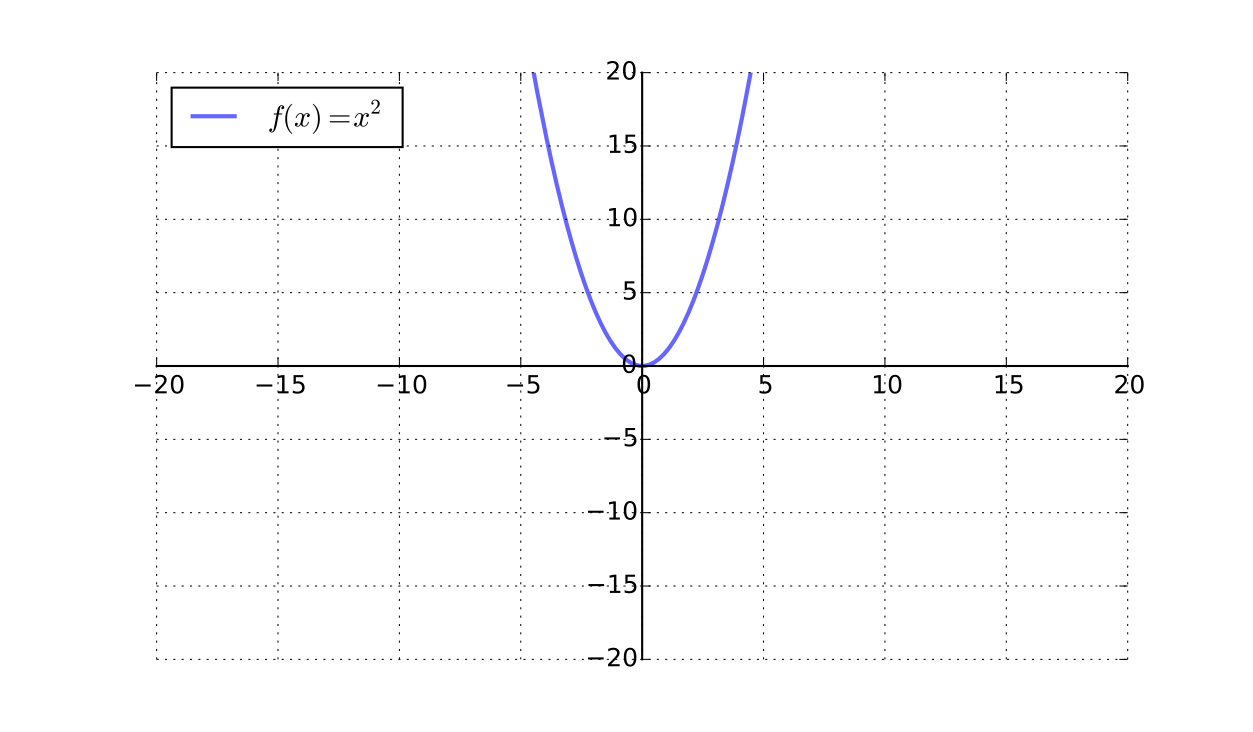
Example

$x \mapsto x^2$ is not a bijection from $\mathbb{R}$ to $\mathbb{R} $

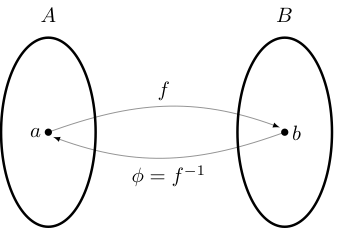
Fact

If $f \colon A \to B$ a bijection, then there exists a unique function $\phi \colon B \to A$ such that

\[ \phi(f(a)) = a, \quad \forall \; a \in A \]

That function $\phi$ is called the inverse of $f$ and written $f^{-1}$

Example

Let

$f \colon \mathbb{R} \to (0, \infty)$ be defined by $f(x) = \exp(x) := e^x$
$\phi \colon (0, \infty) \to \mathbb{R}$ be defined by $\phi(x) = \log(x)$

Then $\phi = f^{-1}$ because, for any $a \in \mathbb{R}$,

\[ \phi(f(a)) = \log(\exp(a)) = a \]

Fact

If $f \colon A \to B$ is one-to-one, then $f \colon A \to \mathrm{rng}(f)$ is a bijection

Fact

Let $f \colon A \to B$ and $g \colon B \to C$ be bijections

$f^{-1}$ is a bijection and its inverse is $f$

$f^{-1}(f(a)) = a$ for all $a \in A$
$f(f^{-1}(b)) = b$ for all $b \in B$
$g \circ f$ is a bijection from $A$ to $C$ and $(g \circ f)^{-1} = f^{-1} \circ g^{-1}$

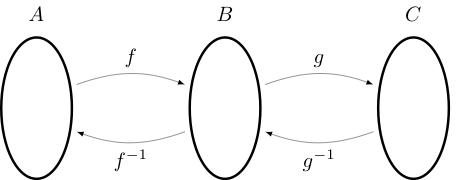
_images/bij_inv.png — Fig. 29 Illustration of $(g \circ f)^{-1} = f^{-1} \circ g^{-1}$#

Cardinality#

If a bijection exists between sets $A$ and $B$ they are said to have the same cardinality, and we write $|A| = |B|$

Fact

If $|A| = |B|$ and $A$ and $B$ are finite then $A$ and $B$ have the same number of elements (same cardinality).

Exercise: Convince yourself this is true

Hence “same cardinality” is analogous to “same size”

But cardinality applies to infinite sets as well!

Fact

If $|A| = |B|$ and $|B| = |C|$ then $|A| = |C|$

Proof

Since $|A| = |B|$, there exists a bijection $f \colon A \to B$
Since $|B| = |C|$, there exists a bijection $g \colon B \to C$

Let $h := g \circ f$

Then $h$ is a bijection from $A$ to $C$

Hence $|A| = |C|$

Definition

A nonempty set $A$ is called finite if

\[ |A| = |\{1, 2, \ldots, n\}| \quad \text{ for some } \quad n \in \mathbb{N} \]

Otherwise called infinite

Definition

Sets that either are finite, or have the same cardinality as $\mathbb{N}$ (denoted $|A| = \aleph_0$) are called countable.

Example

$-\mathbb{N} := \{\ldots, -4, -3, -2, -1\}$ is countable

\[\begin{split} \begin{array}{ccc} -1 & \leftrightarrow & 1 \\ -2 & \leftrightarrow & 2 \\ -3 & \leftrightarrow & 3 \\ & \vdots & \\ -n & \leftrightarrow & n \\ & \vdots & \end{array} \end{split}\]

Formally: $f(k) = -k$ is a bijection from $-\mathbb{N}$ to $\mathbb{N}$

Example

$E := \{2, 4, \ldots\}$ is countable

\[\begin{split} \begin{array}{ccc} 2 & \leftrightarrow & 1 \\ 4 & \leftrightarrow & 2 \\ 6 & \leftrightarrow & 3 \\ & \vdots & \\ 2n & \leftrightarrow & n \\ & \vdots & \end{array} \end{split}\]

Formally: $f(k) = k/2$ is a bijection from $E$ to $\mathbb{N}$

Example

$\{100, 200, 300, \ldots\}$ is countable

\[\begin{split} \begin{array}{ccc} 100 & \leftrightarrow & 1 \\ 200 & \leftrightarrow & 2 \\ 300 & \leftrightarrow & 3 \\ & \vdots & \\ 100n & \leftrightarrow & n \\ & \vdots & \end{array} \end{split}\]

Fact

Nonempty subsets of countable sets are countable

Fact

Finite unions of countable sets are countable

Sketch of proof, for

$A$ and $B$ countable $\implies A \cup B$ countable
$A$ and $B$ are disjoint and infinite

By assumption, can write $A = \{a_1, a_2, \ldots\}$ and $B = \{b_1, b_2, \ldots\}$

Now count it like so:

\[\begin{split} \begin{matrix} a_1 & & a_2 & & a_3 & & a_4 & \cdots\\ \downarrow & \nearrow & \downarrow & \nearrow & \downarrow & \nearrow & \downarrow & \nearrow \\ b_1 & & b_2 & & b_3 & & b_4 & \cdots \end{matrix} \end{split}\]

Example

$\mathbb{Z} = \{\ldots, -2, -1\} \cup \{ 0 \} \cup \{1, 2, \ldots\}$ is countable

Fact

Finite Cartesian products of countable sets is countable

Sketch of proof, for

$A$ and $B$ countable $\implies A \times B$ countable
$A$ and $B$ are disjoint and infinite

Now count like so:

\[\begin{split} \begin{matrix} (a_{1},b_{1})&\to &(a_{1},b_{2})& & (a_{1},b_{3})&\to\cdots\\ &\swarrow& &\nearrow & & \\ (a_{2},b_{1})& &(a_{2},b_{2})& &\cdots & \\ \downarrow &\nearrow& & & & \\ (a_{3},b_{1})& &\vdots & & & \\ \vdots & & & & & \end{matrix} \end{split}\]

Example

$\mathbb{Z} \times \mathbb{Z} = \{ (p,q) : p \in \mathbb{Z}, q \in \mathbb{Z} \}$ is countable

Fact

$\mathbb{Q}$ is countable

Proof

By definition

\[ \mathbb{Q}:= \left\{ \, \text{all } \frac{p}{q} \text{ where } p \in \mathbb{Z} \text{ and } q \in \mathbb{N} \, \right\} \]

Consider the function $\phi$ defined by $\phi(p/q) = (p, q)$

A one-to-one function from $\mathbb{Q}$ to $\mathbb{Z} \times \mathbb{N}$
A bijection from $\mathbb{Q}$ to $\mathrm{rng}(\phi)$

Since $\mathbb{Z} \times \mathbb{N}$ is countable, so is $\mathrm{rng}(\phi) \subset \mathbb{Z} \times \mathbb{N}$

Hence $\mathbb{Q}$ is also countable

Example

An example of an uncountable set is all binary sequences

\[ \{0,1\}^{\mathbb{N}} := \big\{ (b_1,b_2,\ldots) : \, b_n \in \{0,1\ \} \text{ for each } n \big\} \]

Sketch of proof: If this set were countable then it could be listed as follows:

\[\begin{split} \begin{matrix} 1 & \leftrightarrow & {\bf a_1}, \; a_2, \; a_3, \; a_4, \ldots \\ 2 & \leftrightarrow & b_1, \;{\bf b_2}, \; b_3, \; b_4, \ldots \\ 3 & \leftrightarrow & c_1, \; c_2, \;{\bf c_3}, \; c_4, \ldots \\ 4 & \leftrightarrow & d_1, \; d_2, \; d_3, \;{\bf d_4}, \ldots \\ \vdots & & \vdots \end{matrix} \end{split}\]

Such a list is never complete: Cantor’s diagonalization argument

Cardinality of $\{0,1\}^{\mathbb{N}}$ called the power of the continuum

Other sets with the power of the continuum

$\mathbb{R}$
$(a, b)$ for any $a < b$
$[a, b]$ for any $a < b$
$\mathbb{R}^N$ for any finite $N \in \mathbb{N}$

Continuum hypothesis

Every nonempty subset of $\mathbb{R}$ is either countable or has the power of the continuum

Not a homework exercise!

Example

$\mathbb{R}$ and $(-1, 1)$ have the same cardinality because $x \mapsto 2\arctan(x)/\pi$ is a bijection from $\mathbb{R}$ to $(-1, 1)$

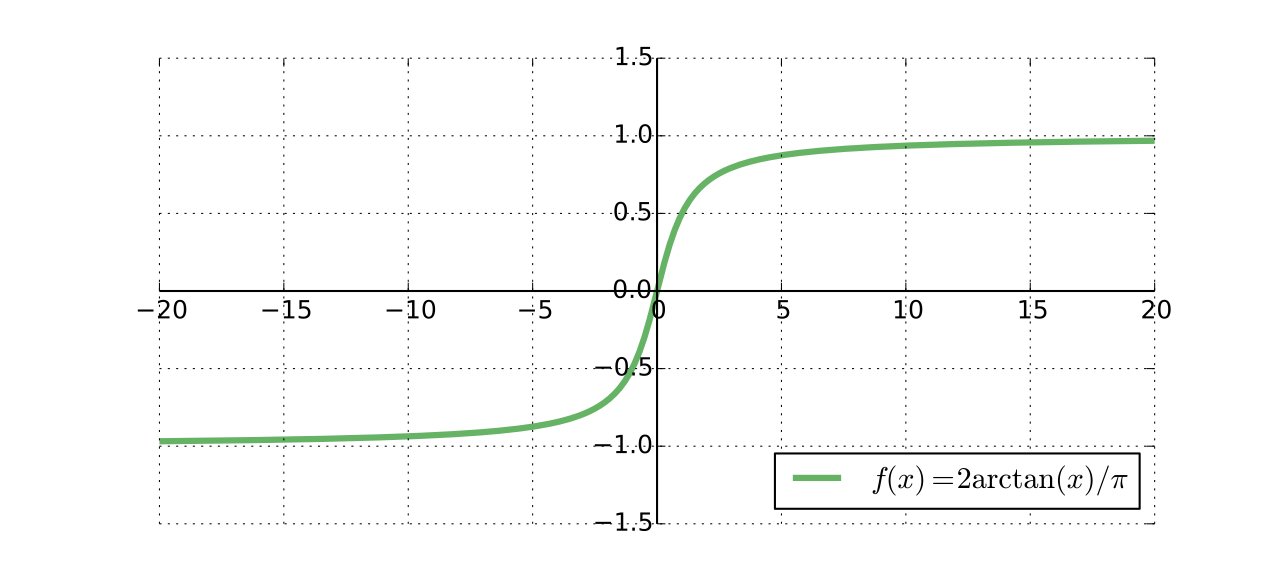
_images/arctan.png — Fig. 30 Same cardinality#

Extra material#

Veritasium video on paradoxes of set theory and mathematical incompleteness YouTube

Elements of set theory

Contents

Elements of set theory#

Logic#

Proof by contradiction#

Sets#

Intervals of \(\mathbb{R}\)#

Operations with sets#

Set operations properties#

Infinite Unions and Intersections#

Tuples#

Cartesian Products#

Counting Finite Sequences#

Counting Cartesian Products#

Functions#

Onto Functions (Surjections)#

One-to-One Functions (Injections)#

Bijections#

Cardinality#

Extra material#