Ctrl+K

🔬 Tutorial problems kappa

🔬 Tutorial problems kappa#

Hide code cell content 
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from myst_nb import glue


f = lambda x: x[0]**3/3 - 3*x[1]**2 + 2*x[0]
gx = lambda y: y**3/4
gy = lambda x: (4*x)**(1/3)

x = y = np.linspace(-5.0, 5.0, 100)
X, Y = np.meshgrid(x, y)
zs = np.array([f((x,y)) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)

ymax = gy(5.0)
y = np.linspace(-ymax, ymax, 100)
X1,Y1 = gx(y),y
zs = np.array([f((x,y)) for x,y in zip(np.ravel(X1), np.ravel(Y1))])
Z1 = zs.reshape(X1.shape)

fig = plt.figure(dpi=160)
ax1 = fig.add_subplot(111)
ax1.set_aspect('equal', 'box')
ax1.contour(X, Y, Z, 50,
            cmap=cm.jet)
ax1.plot(X1, Y1)
plt.setp(ax1, xticks=[],yticks=[])
glue("pic1", fig, display=False)

fig = plt.figure(dpi=160)
ax2 = fig.add_subplot(111, projection='3d')
ax2.plot_wireframe(X, Y, Z,
            rstride=2,
            cstride=2,
            alpha=0.7,
            linewidth=0.25)
f0 = f(np.zeros((2)))+0.1
ax2.plot(X1, Y1, Z1, c='red')
plt.setp(ax2,xticks=[],yticks=[],zticks=[])
ax2.view_init(elev=18, azim=-160)
glue("pic2", fig, display=False)
_images/7dc409c94f0b63d54dcae7f8967370896cd296aca3d791749993476116339ee0.png _images/1c0410363fcfc5de81dbd7da325743a01f8d36fde44dbad4e64d2674d54dafd3.png

\(\kappa\).1#

Solve the following constrained maximization problem using the Lagrange method, including the second order conditions.

\[\begin{split} f(x,y) = \frac{x^3}{3}-3y^2+2x \to \max_{x,y} \\ \text {subject to} \\ 4x = y^3,\\ x,y \in \mathbb{R} \end{split}\]

Follow standard algorithm of Lagrange method.

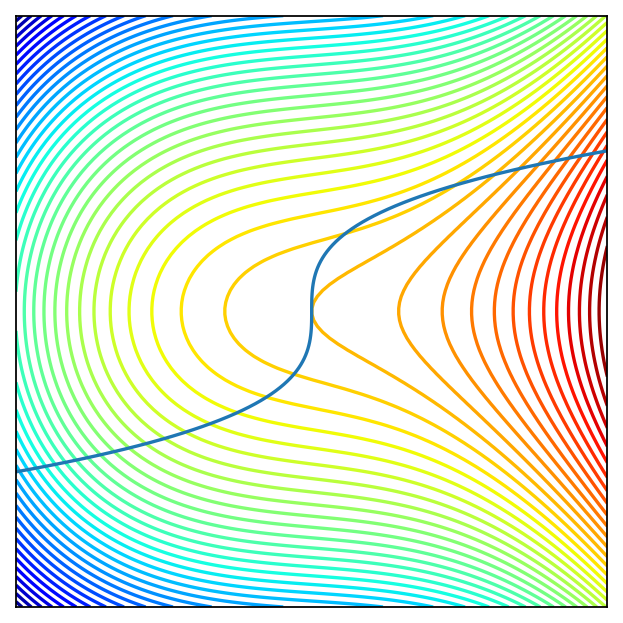
_images/7dc409c94f0b63d54dcae7f8967370896cd296aca3d791749993476116339ee0.png

Fig. 95 Level curves of the criterion function and constraint curve.#

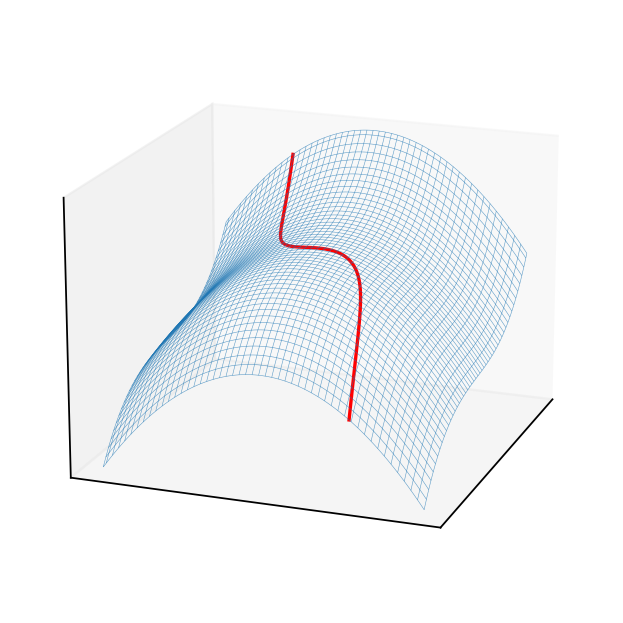
_images/1c0410363fcfc5de81dbd7da325743a01f8d36fde44dbad4e64d2674d54dafd3.png

Fig. 96 3D plot of the criterion surface with the constraint curve projected to it.#

⏱

\(\kappa\).2#

Find the maxima and minima of the function

\[ f(x,y) = xy \text{ subject to } x^2+y^2=2a^2, a>0 \]

Check both first and second order conditions.

Follow standard algorithm of Lagrange method.

⏱

\(\kappa\).3#

Find the maxima and minima of the function

\[ f(x,y) = \tfrac{1}{x} + \tfrac{1}{y} \]

subject to

\[ (\tfrac{1}{x})^2+(\tfrac{1}{y})^2=(\tfrac{1}{a})^2, \]

where \(a>0\).

Follow standard algorithm of Lagrange method.

⏱

\(\kappa\).4#

Solve the following maximization problem

\[\begin{split} xy^{\tfrac{1}{2}}z^{\tfrac{1}{3}} \longrightarrow max_{x,y,z} \\ \text{ subject to }\quad\quad\\ x \ge 0, y \ge 0 ,z \ge 0,\\ 3x + 2y + z \le 10\\ \end{split}\]

Follow standard algorithm of Lagrange method.

⏱

Contents