📖 Quadratic forms#
⏱ | words
Conic sections#
Conic sections are a collection of curves obtained by intersecting a cone with a plane.
An equation describing every conic section is a quadratic equation in two variables.

Fig. 68 Conic sections#
Definition
A collection of points \((x,y)\in\mathbb{R}^2\), the sum of distances from which to two fixed points (termed foci) is constant, is an ellipse.
When the two foci coincide, the ellipse becomes a circle.
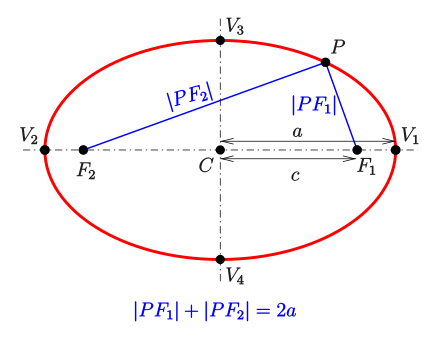
Canonical equation of an ellipse with parameters \(a\) and \(b\)
When \(a=b\), the ellipse becomes a circle with radius \(a=b\).
Definition
Parabola is a collection of points \((x,y)\in\mathbb{R}^2\) laying at equal distances from a fixed point (focus) and a fixed line (directrix).
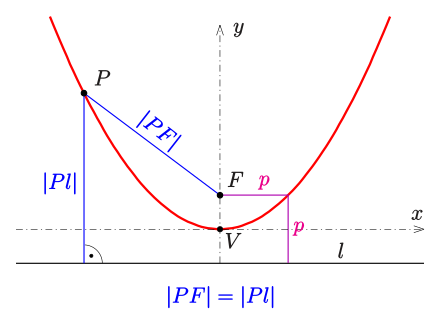
Parabola is a section of a cone by a plane parallel to another plane tangential to the conical surface.
Canonical equation of an ellipse with parameters \(a\) and \(b\)
Definition
Hyperbola is a collection of points \((x,y)\in\mathbb{R}^2\), the difference of distances from which to two fixed points (termed foci) is constant.
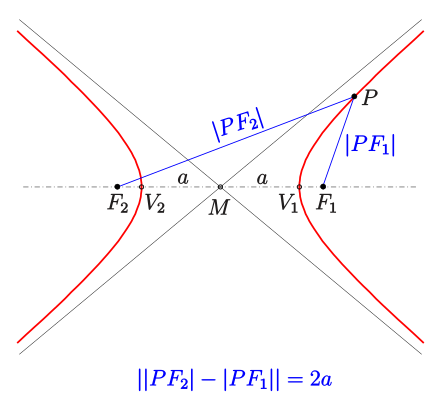
Canonical equation of an ellipse with parameters \(a\) and \(b\)
We typically encounter a hyperbola with the equation \(y=1/x\) or \(yx=1\), but it is easy to show that this is a special case with \(a=b\) after a change of basis with transformation matrix given by \(P=\tfrac{1}{\sqrt{2}}\begin{pmatrix}1&-1\\1&1\end{pmatrix}\)
Note
The highest power of \(x\) and \(y\) in the equation of a conic section is 2, hence the name quadratic curves.
Quadratic forms#
Definition
Quadratic form in a function \(Q \colon \mathbb{R}^N \to \mathbb{R}\)
Note that we can assume that \(a_{ij} = a_{ji}\): indeed, if for some quadratic form \(\sum_{i=1}^N \sum_{j=1}^N c_{ij} x_i x_j\) symmetry does not hold, redefine
then
Definition
Quadratic form \(Q \colon \mathbb{R}^N \to \mathbb{R}\) can be equivalently represented as a matrix product
where \(x \in \mathbb{R}^N\) is a column vector, and \((N \times N)\) symmetric matrix \(A\) consists of elements \(\{a_{ij}\}\), \(i,j=1,\ldots,N\)
Example
has a matrix representation with
Exercise: verify
Note
The degree of a quadratic form \(Q(x)\) which is a multivariate polynomial function is given by the sum of the powers of the variables, and for quadratic forms is not higher than 2, hence the name quadratic form. This implies that no term of the quadratic form may have a product of more than two variables!
Why are quadratic forms useful in the optimization course?
Look at the third term in the multivariate Taylor expansion of a function \(f(x) \colon \mathbb{R}^N \to \mathbb{R}\). It is a quadratic form!
We use quadratic forms for a local approximation of any function, in particular the functions we will want to optimize — later in the course.
Canonical form of quadratic forms#
Definition
A canonical form of a quadratic form \(Q(x)\) is given by a sum of squares of the variables
Fact
By change of bases any quadratic form \(Q(x)\) with a symmetric real matrix \(A\) can be transformed to a sum of squares with positive or negative coefficients
where \(\lambda_i\) are the eigenvalues and \(P\) is the matrix of eigenvectors of \(A\).
Proof
It follows from the symmetry of \(A\) that it has \(N\) real eigenvalues and can be diagonalized with the transformation matrix \(P\) composed of eigenvectors.
The change of variable \(y = Px\) leads to a transformed quadratic form \(Q(y) = y^T D y = \sum_{i=1}^N \lambda_i y_i^2\) which contains only squares of the variables.
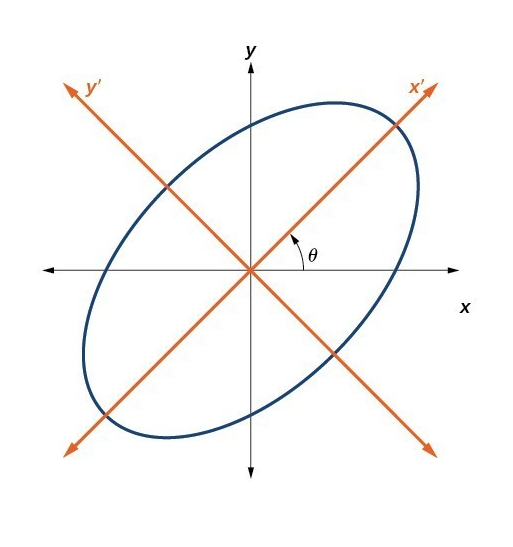
Fig. 69 Change of bases to convert the quadratic form to a canonical form#
Definiteness of quadratic forms#
The properties and shape of \(Q(x)\) depend on the configuration of matrix \(A\)
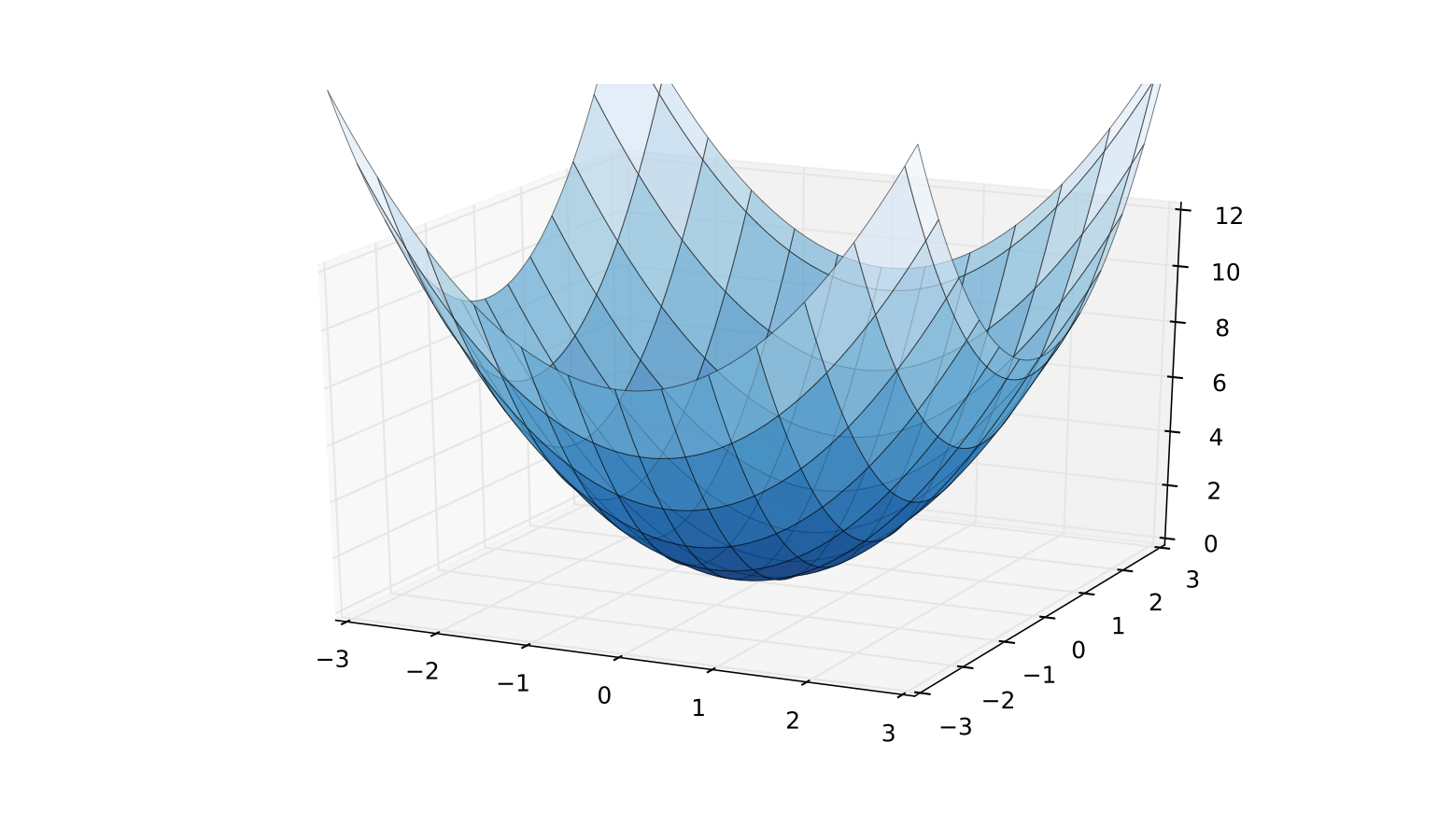
Fig. 70 A convex \(Q(x) = x' I x\)#
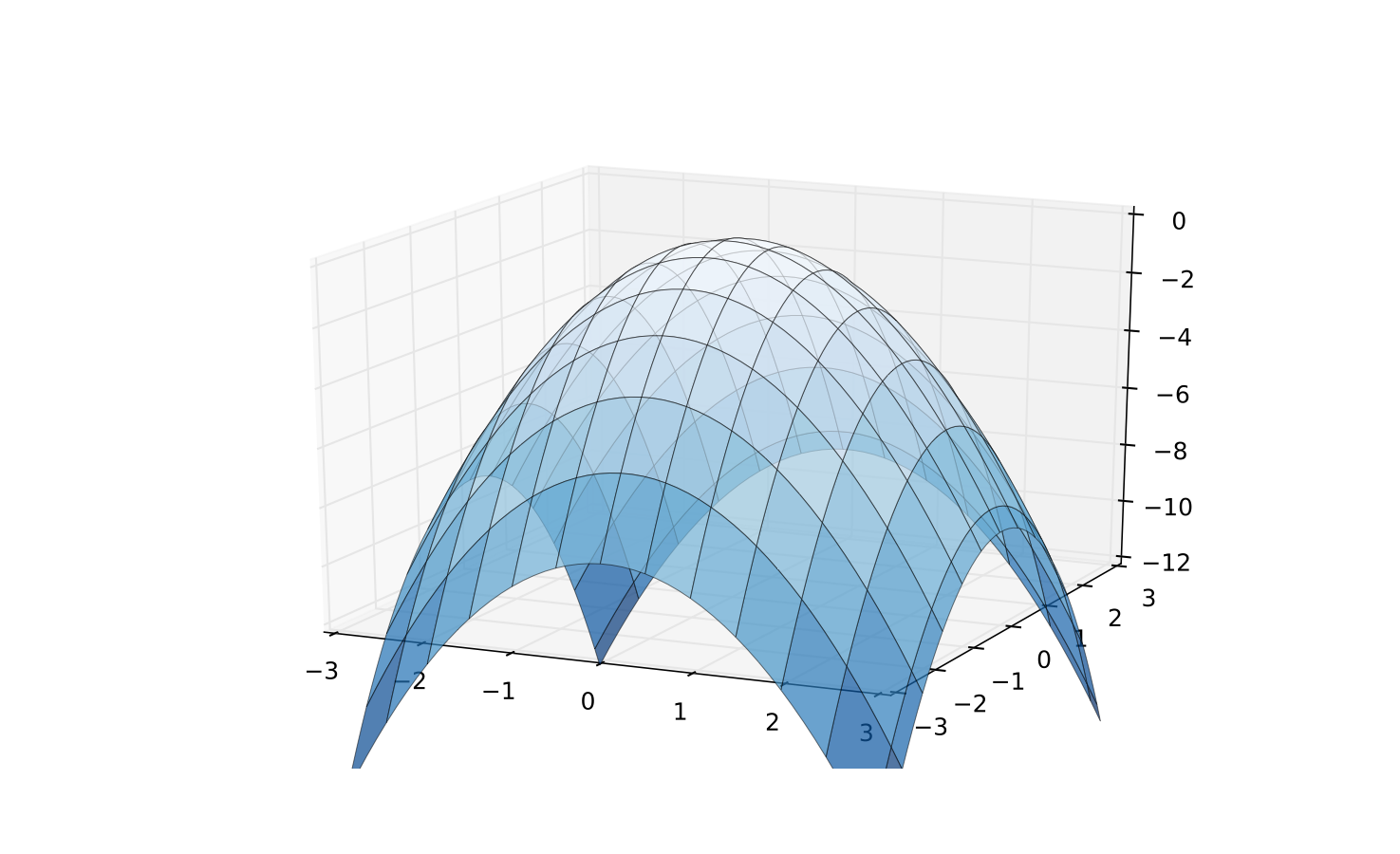
Fig. 71 A concave \(Q(x) = x'(-I)x\)#
Definition
Quadratic form \(Q(x)\) is called positive definite if
Quadratic form \(Q(x)\) is called negative definite if
the examples above show these cases
note that because every quadratic form can be represented by a linear combination of squares, the characteristic properties are the signs of the coefficients in the canonical form!
Fact (Law of inertia)
The number of coefficients of a given sign in the canonical form of a quadratic form does not depend on the choice of the basis
such robust characteristics are called invariants
number of coefficients of a given sign is an invariant of the quadratic form called the index of the quadratic form
Definition
Positive and negative definite quadratic forms are called definite
Note that for some matrices it may be that
for some \(x\): \(x^T A x < 0\)
for some \(x\): \(x^T A x > 0\)
In this case \(A\) is called indefinite
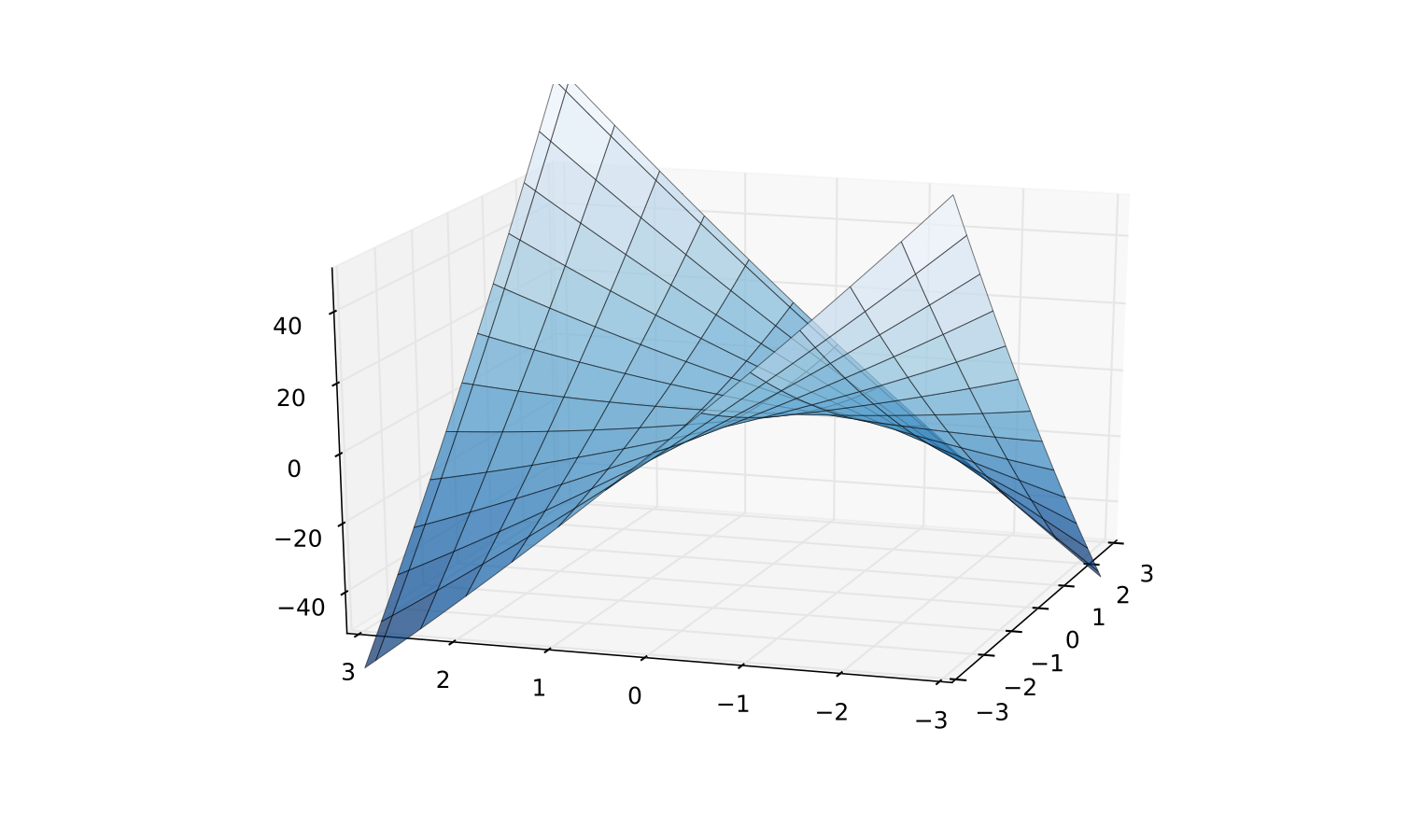
Fig. 72 Indefinite quadratic function \(Q(z) = x_1^2/2 + 8 x_1 x_2 + x_2^2/2\)#
Example
Definition
Quadratic form \(Q(x)\) is called non-negative definite (positive semi-definite) if
Quadratic form \(Q(x)\) is called non-positive definite (negative semi-definite) if
Example
In the last example, the points \(t(1,-1)\) for any \(t \in \mathbb{R}\) yield \(Q(x) = 0\)
Fact (eigenvalues criterion)
A quadratic form \(Q(x)\) with a symmetric real matrix \(A\) is
positive definite \(\iff\) all eigenvalues are strictly positive
negative definite \(\iff\) all eigenvalues are strictly negative
nonpositive definite \(\iff\) all eigenvalues are nonpositive
nonnegative definite \(\iff\) all eigenvalues are nonnegative
Proof
Follows immediately from the diagonalization of \(A\) \(\blacksquare\)
Example
Let’s diagonalize \(A\) by finding eigenvalues and eigenvectors
Eigenvalues are \(\lambda_1 = 1\) and \(\lambda_2 = 36\)
Eigenvectors are \(v_1 = (2,1)\) and \(v_2 = (-1,2)\)
Transformation matrix is \(P = \begin{pmatrix} 2 & -1 \\ 1 & 2 \end{pmatrix}\)
Let \((u,v) = (2x-y,x+2y)\), then the quadratic form can be written as \(Q(u,v) = u^2 + 36v^2 >0\) for any \(u,v\)
Hense, \(Q(x)\) is a positive definite
Fact
If quadratic form \(x^TAx\) is positive definite, then \(\det(A) > 0\)
Proof
Positive definite \(\iff\) all eigenvalues are strictly positive \(\implies\) \(det(A)>0\) as the product of eigenvalues. \(\blacksquare\)
in particular, \(A\) is nonsingular
Silvester’s criterion#
Diagonalization of the higher order matrices may be hard. We have an alternative for determining the definiteness of a quadratic form
Definition
Consider a \(N \times N\) matrix \(A\) and let \(0 < k \le N\).
The leading principal minor \(M_k\) of order \(k\) of \(A\) is the determinant of a matrix obtained from \(A\) by deleting its last \(N-k\) rows and columns.
Example
The leading principal minors of oder \(k = 1,\dots,n\) of \(A\) are
Fact (definiteness)
Let \(A\) be an \((N \times N)\) symmetric square matrix. The corresponding quadratic form \(Q(x) = x^T A x\) is positive definite if and only if all leading principal minors of \(A\) are positive
Quadratic form \(Q(x) = x^T A x\) is negative definite if and only if the leading principal minors of \(A\) alternate in sign according to the following rule
the last condition can be restated as the leading principle minor \(M_k\) to have the same sign as \((-1)^k\)
if \(A\) does not satisfy either of the conditions, it is indefinite or semi-definite
Silvester’s criterion for semi-definiteness is more involved
Definition
Consider a \(N \times N\) matrix \(A\) and let \(0 < k \le N\).
The principal minor \(P_k\) of order \(k\) of \(A\) is the determinant of a matrix obtained from \(A\) by deleting any of its \(N-k\) rows and columns with the same indexes.
observe the difference from the leading principal minor
Example
All the principal minors of oder \(k = 1,2,3\) of \(A\) are
Fact (semi-definiteness)
Let \(A\) be an \((N \times N)\) symmetric square matrix. The corresponding quadratic form \(Q(x) = x^T A x\) is positive semi-definite if and only if all principal minors of \(A\) are non-negative.
Quadratic form \(Q(x) = x^T A x\) is negative semi-definite if and only if all principal minors of oder \(k\) of \(A\) are zero or have the same sign as \((-1)^k\)
Example
The leading principal minors of \(A\) are
All leading principal minors are positive, hence \(x^TAx\) is positive definite.
It can also be shown that the eigenvalues of \(A\) are \(\{1,2,3\}\), that is all positive, and therefore the same conclusion is reached by the eigenvalues criterion.
Example
The leading principal minors of \(B\) are
The leading principal minors do not match neither the rule for positive definiteness (all positive) nor the rule for negative definiteness (alternating signs). But the rule for the negative semi-definiteness may still be satisfied, hence let’s examine the rest of principal minors.
The other (non-leading) principal minors of order \(k=1\) of \(B\) are
and it is clear that the rule for negative semi-definiteness is not satisfied: principle minors of oder 1 differ in signs.
Thus, \(x^TBx\) is indefinite.
It can also be shown that the eigenvalues of \(A\) are \(\{-\sqrt{2},0,\sqrt{2}\}\), that is they differ is sing, and therefore \(B\) is indefinite also by the eigenvalues criterion.
Example
The leading principal minors of \(C\) are
The leading principal minors do not match neither the rule for positive definiteness (all positive) nor the rule for negative definiteness (alternating signs). But the rule for the negative semi-definiteness may still be satisfied, hence let’s examine the rest of principal minors, namely one more principle minor of order 1:
Ok, the pattern for negative semi-definiteness is satisfied!
Thus, \(x^TCx\) is negative semi-definite.
The plot of the quadratic form \(x^TCx\) is below. Note the line of zero values of the quadratic form attained at many different non-zero points \((-p,p/\sqrt{2})\), where \(p \in \mathbb{R}\).
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
A = np.array([[-1,-np.sqrt(2)],[-np.sqrt(2),-2]])
f = lambda x: x@A@x
x = y = np.linspace(-5.0, 5.0, 100)
X, Y = np.meshgrid(x, y)
zs = np.array([f((x,y)) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)
fig = plt.figure(dpi=160)
ax3 = fig.add_subplot(111, projection='3d')
ax3.plot_wireframe(X, Y, Z,
rstride=2,
cstride=2,
alpha=0.7,
linewidth=0.25)
f0 = f(np.zeros((2)))+0.1
ax3.plot([-5,5],[5/np.sqrt(2),-5/np.sqrt(2)],[f0,f0],color='black',linewidth=0.5)
plt.setp(ax3,xticks=[],yticks=[],zticks=[])
plt.show()
References and reading#
References
[Simon and Blume, 1994]: 13.3, 16.1, 16.2
[Sundaram, 1996]: 1.5
Further reading and self-learning
Excellent visualizations of concepts covered in this lecture, strongly recommended for further study 3Blue1Brown: Essence of linear algebra

