Ctrl+K

🔬 Problem set alpha

🔬 Problem set alpha#

\(\alpha\).1#

Consider the statement All students taking ECON6012 class are admitted at ANU

  • Write this statement in the form \(P \implies Q\)

  • Is this a true statement?

  • Write down the converse of the statement. Is it true?

  • Write down the contrapositive for the statement. Is it true?

Review the definitions of the terms converse and contrapositive.

⏱

\(\alpha\).2#

This is an exercise on necessary and sufficient conditions. Start with some definitions from geormetry:

  • a quadrilateral is a planar figure made up of four line segments connected to form a closed shape. Consider only simple quadrilaterals without self-intersections.

  • a quadrilateral with a pair of parallel sides is called a trapezoid

  • a quadrilateral with two pais of parallel sides is called a parallelogram

  • a parallelogram with right angles is called a rectangle

  • a rectangle with all sides of the same length is called a square

  • a parallelogram with all sides of the same length is called a rhombus

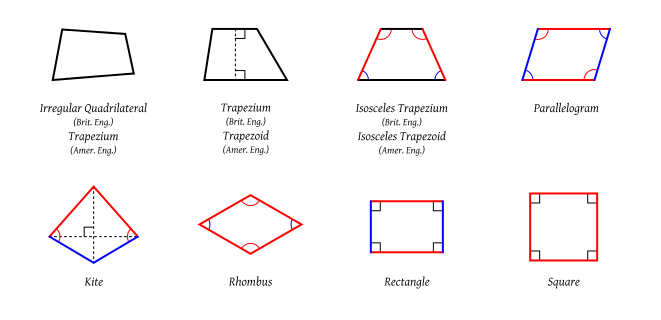
illustration

For each of the statements below determine if they are True or False. For those which are False, provide a counterexample.

  1. Sufficient condition for a quadrilateral to be a square is for it to be a rhombus.

  2. Necessary condition for a quadrilateral to be a square is for it to be a rectangle.

  3. Sufficient condition for a quadrilateral to be a rectangle is for it to be a parallelogram.

  4. Necessary condition for a quadrilateral to be a rectangle is for it to be a parallelogram.

  5. Necessary condition for a quadrilateral to be a parallelogram is for it to be a trapezoid.

  6. Sufficient condition for a quadrilateral to be a parallelogram is for it to be a square.

  7. Necessary condition for a quadrilateral to be a trapezoid is for it to be a rhombus.

  8. Necessary condition for a quadrilateral to be a rectangle is for it to be a trapezoid.

  9. Necessary and sufficient conditions for a quadrilateral to be a square are for it to simultaneously be a rectangle and a rhombus.

⏱

\(\alpha\).3#

Using direct proof, show that the difference between a cube of a natural number greater than one, \(n=2,3,\dots\), and the number itself is divisible by 6.

Factor the expression \(n^3-n\) and use the property of the consecutive natural numbers.

⏱

\(\alpha\).4#

Prove by contradiction that \(\sqrt{3}\) is an irrational number (so that is it can not be represented by a ratio of two whole numbers).

Assume the opposite, namely that \(\sqrt{3} = \frac{p}{q}\) where without loss of generality whole numbers \(p\) and \(q\) do not have common factors.

⏱

\(\alpha\).5#

Using mathematical induction prove that \(n < 2^n\) holds for all natural numbers \(n=1,2,\dots\).

Verify the statement holds for \(n=1\), and assuming \(n<2^n\) prove that \(n+1 < 2^{n+1}\).

⏱

Note

The symbol \(\blacksquare\) marks the end of the proof, and is equivalent to the QED symbol (”quod erat demonstrandum”, or “that which was to be demonstrated”).

Contents