☕️ Numerical equation solving

This chapter is for your information only, will not be part of the assessment

by Fedor Iskhakov

Description: Bisections and Newton-Raphson methods. Solving equations of one variable. Accuracy of solution. Rates of convergence.

YouTube recording of this lecture in the Foundational of Computational Economics course

Classic algorithm for equation solving

1. Bisection method

2. Newton-Raphson method

Solve equations of the form \( f(x) = 0 \)

Focus on the scalar case today.

Bisection method for solving equations

Solve equation \( f(x)=0 \), conditional on \( x \in [a,b] \subset \mathbb{R} \) such that \( f(a)f(b)<0 \)

Algorithm: similar to binary search, but in continuous space.

def bisection(f,a=0,b=1,tol=1e-6,maxiter=100,callback=None):
    '''Bisection method for solving equation f(x)=0
    on the interval [a,b], with given tolerance and number of iterations.
    Callback function is invoked at each iteration if given.
    '''
    if f(a)*f(b)>0:
        raise ValueError('Function has the same sign at the bounds')
    for i in range(maxiter):
        err = abs(b-a)
        if err<tol: break
        x = (a+b)/2
        a,b = (x,b) if f(a)*f(x)>0 else (a,x)
        if callback != None: callback(err=err,x=x,iter=i)
    else:
        raise RuntimeError('Failed to converge in %d iterations'%maxiter)
    return x

f = lambda x: -4*x**3+5*x+1
a,b = -3,-.5  # upper and lower limits
x = bisection(f,a,b)
print('Solution is x=%1.3f, f(x)=%1.12f' % (x,f(x)))

Solution is x=-1.000, f(x)=0.000000834465

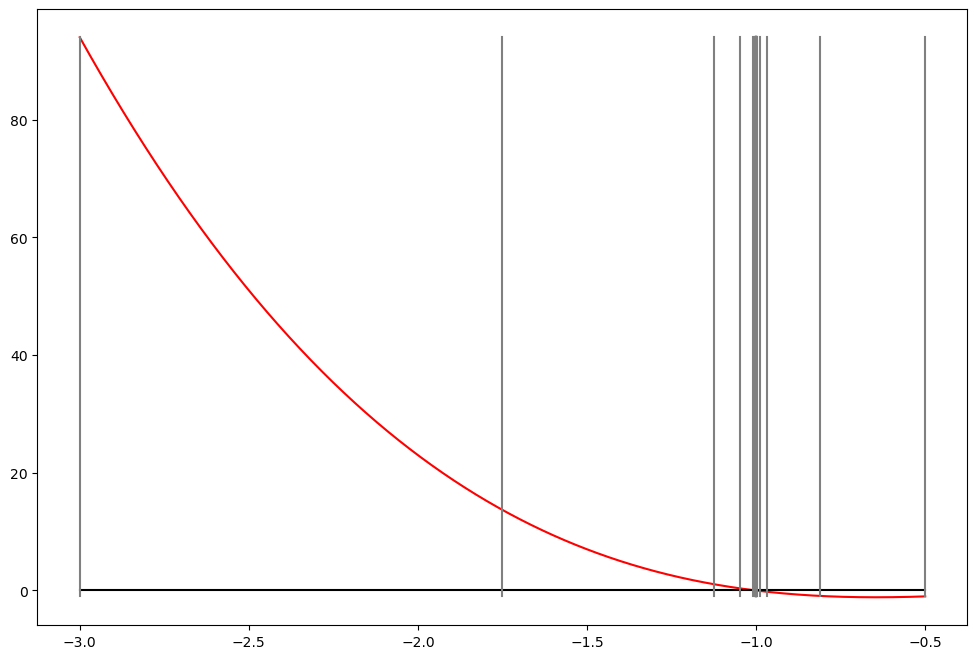
# make nice plot
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = [12, 8]
xd = np.linspace(a,b,1000)  # x grid
plt.plot(xd,f(xd),c='red')  # plot the function
plt.plot([a,b],[0,0],c='black')  # plot zero line
ylim=[f(a),min(f(b),0)]
plt.plot([a,a],ylim,c='grey')  # plot lower bound
plt.plot([b,b],ylim,c='grey')  # plot upper bound
def plot_step(x,**kwargs):
    plot_step.counter += 1
    plt.plot([x,x],ylim,c='grey')
plot_step.counter = 0  # new public attribute
bisection(f,a,b,callback=plot_step)
print('Converged in %d steps'%plot_step.counter)
plt.show()

Converged in 22 steps

Newton-Raphson (Newton) method

General form \( f(x)=0 \)

• Equation solving

• Finding maximum/minimum based on FOC, then \( f(x)=Q'(x) \)

Algorithm:

1. Start with some good guess \( x_0 \) not too far from the solution

2. Newton step: \( x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)} \)

3. Iterate until convergence in some metric

Derivation for Newton method using Taylor series expansion

\[ f(x) = \sum_{k=0}^{\infty} \frac{f^{(k)}(x_0)}{k!} (x-x_0)^k \]

Take first two terms, assume \( f(x) \) is solution, and let \( x_0=x_i \) and \( x=x_{i+1} \)

\[ 0 = f(x) = f(x_i) + f'(x_i) (x_{i+1}-x_i) \quad \Rightarrow \quad x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)} \]

def newton(fun,grad,x0,tol=1e-6,maxiter=100,callback=None):
    '''Newton method for solving equation f(x)=0
    with given tolerance and number of iterations.
    Callback function is invoked at each iteration if given.
    '''
    for i in range(maxiter):
        x1 = x0 - fun(x0)/grad(x0)
        err = abs(x1-x0)
        if callback != None: callback(err=err,x0=x0,x1=x1,iter=i)
        if err<tol: break
        x0 = x1
    else:
        raise RuntimeError('Failed to converge in %d iterations'%maxiter)
    return (x0+x1)/2

f = lambda x: -4*x**3+5*x+1
g = lambda x: -12*x**2+5
x = newton(f,g,x0=-2.5,maxiter=7)
print('Solution is x=%1.3f, f(x)=%1.12f' % (x,f(x)))

Solution is x=-1.000, f(x)=0.000000490965

# make nice seriest of plots
a,b = -3,-.5  # upper and lower limits
xd = np.linspace(a,b,1000)  # x grid
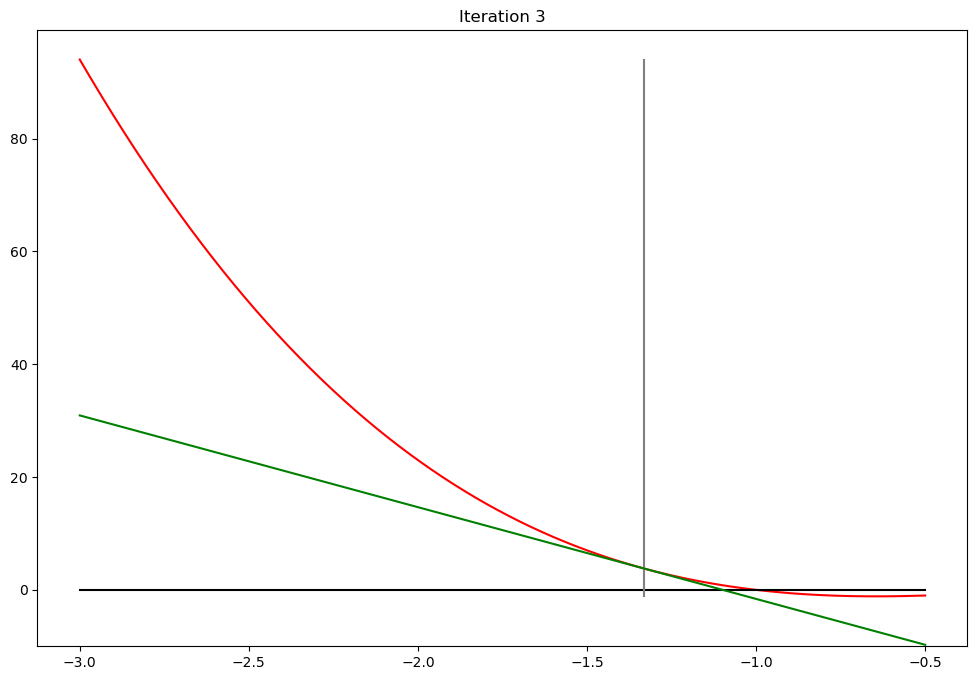
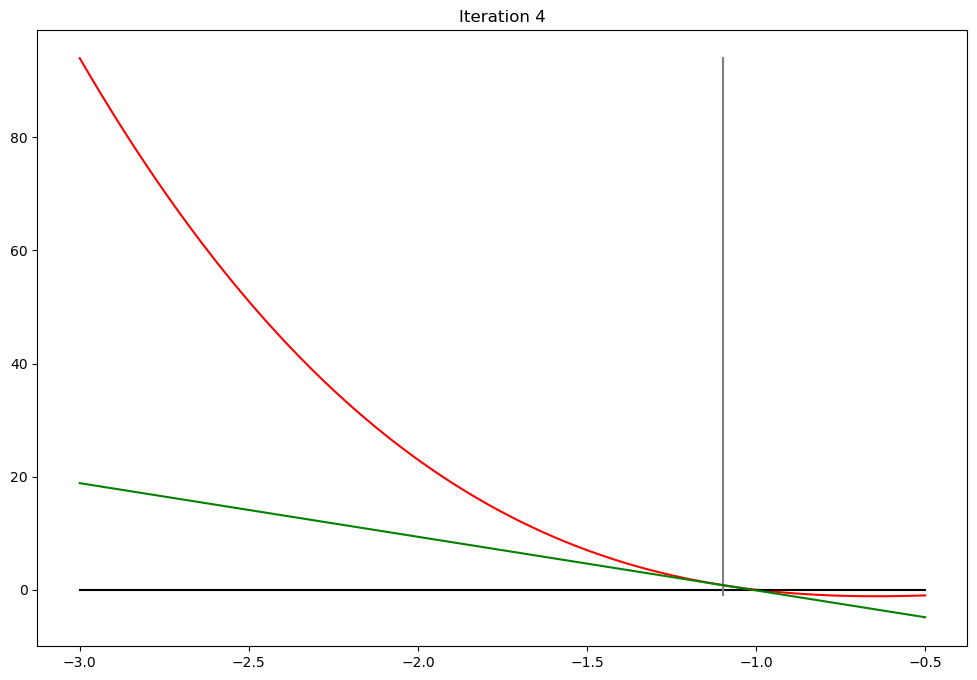
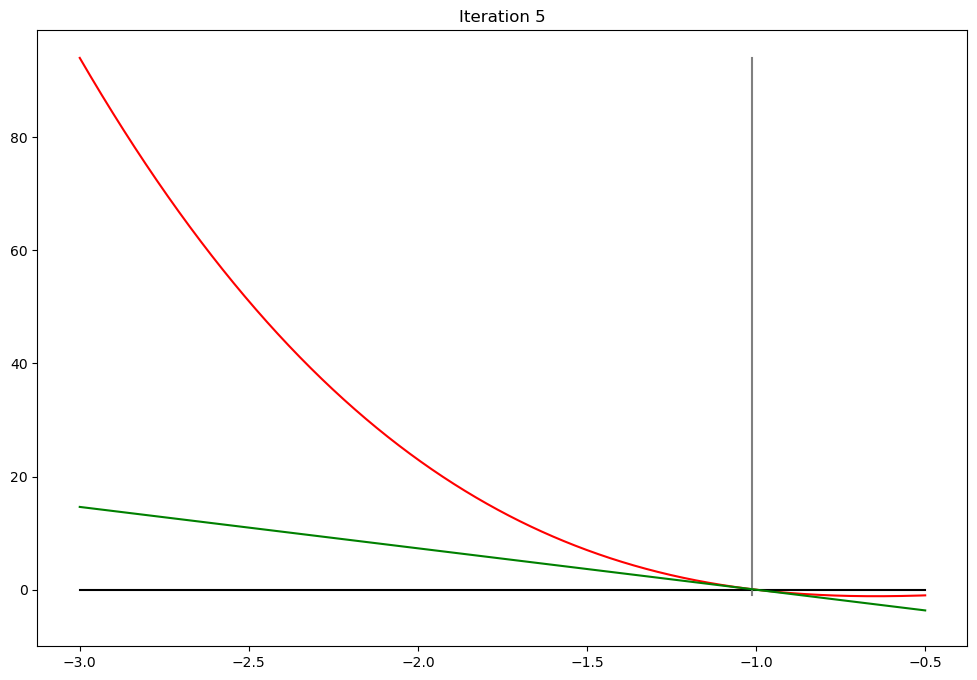
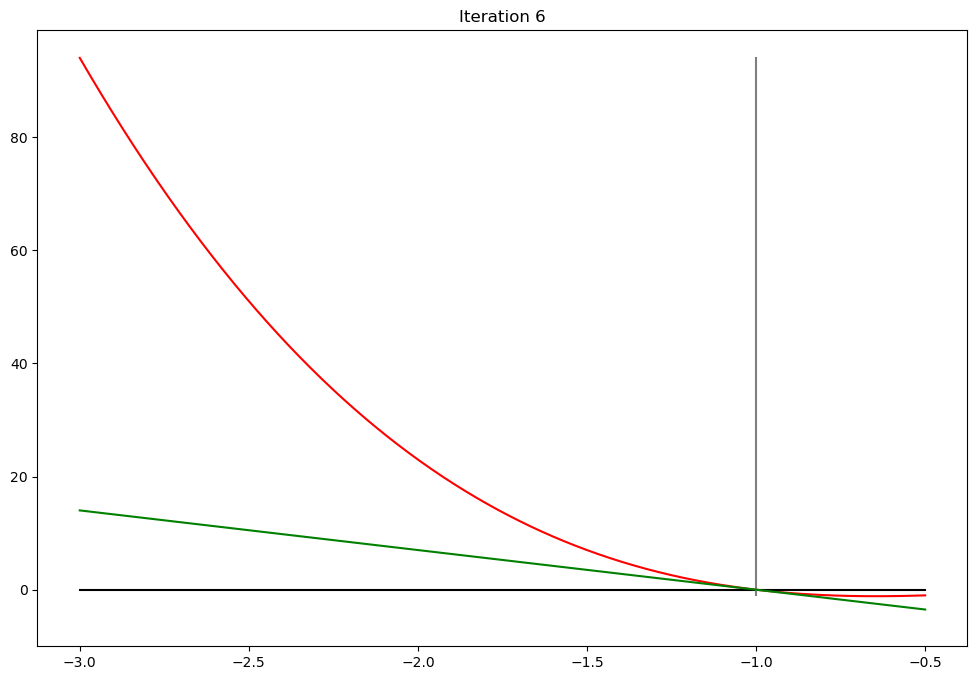
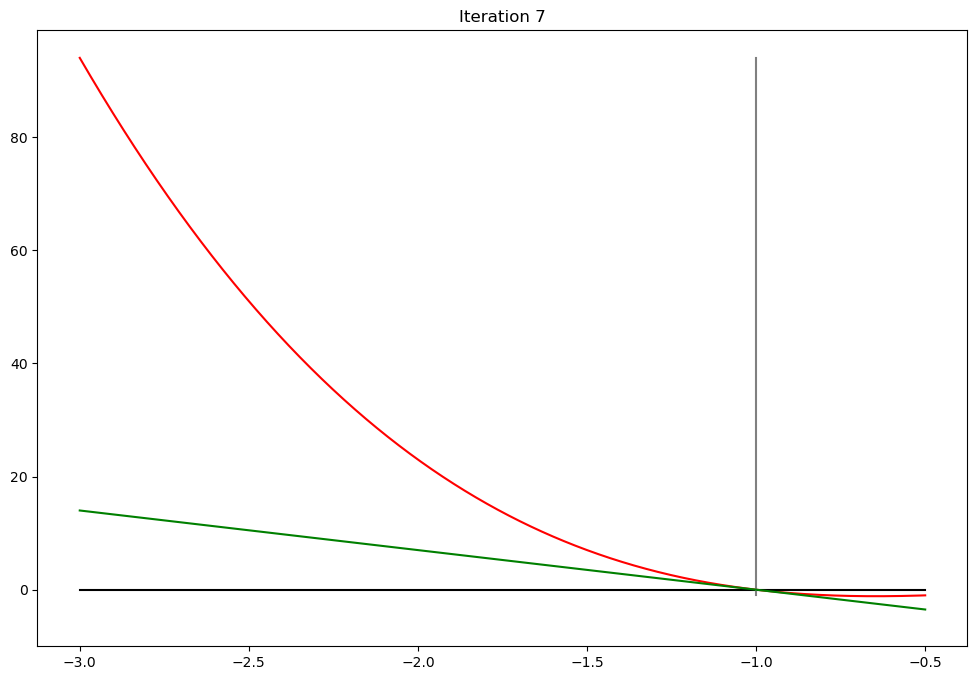
def plot_step(x0,x1,iter,**kwargs):
    plot_step.counter += 1
    if iter<10:
        plt.plot(xd,f(xd),c='red')  # plot the function
        plt.plot([a,b],[0,0],c='black')  # plot zero line
        ylim = [min(f(b),0),f(a)]
        plt.plot([x0,x0],ylim,c='grey') # plot x0
        l = lambda z: g(x0)*(z - x1)
        plt.plot(xd,l(xd),c='green')  # plot the function
        plt.ylim(bottom=10*f(b))
        plt.title('Iteration %d'%(iter+1))
        plt.show()
plot_step.counter = 0  # new public attribute
newton(f,g,x0=-2.5,callback=plot_step)
print('Converged in %d steps'%plot_step.counter)

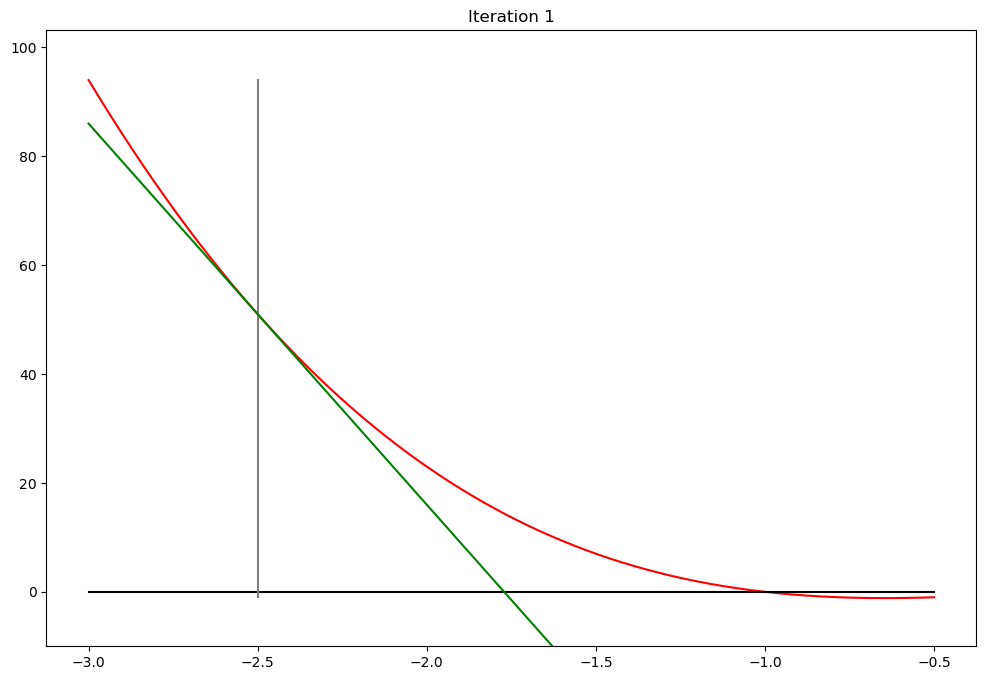
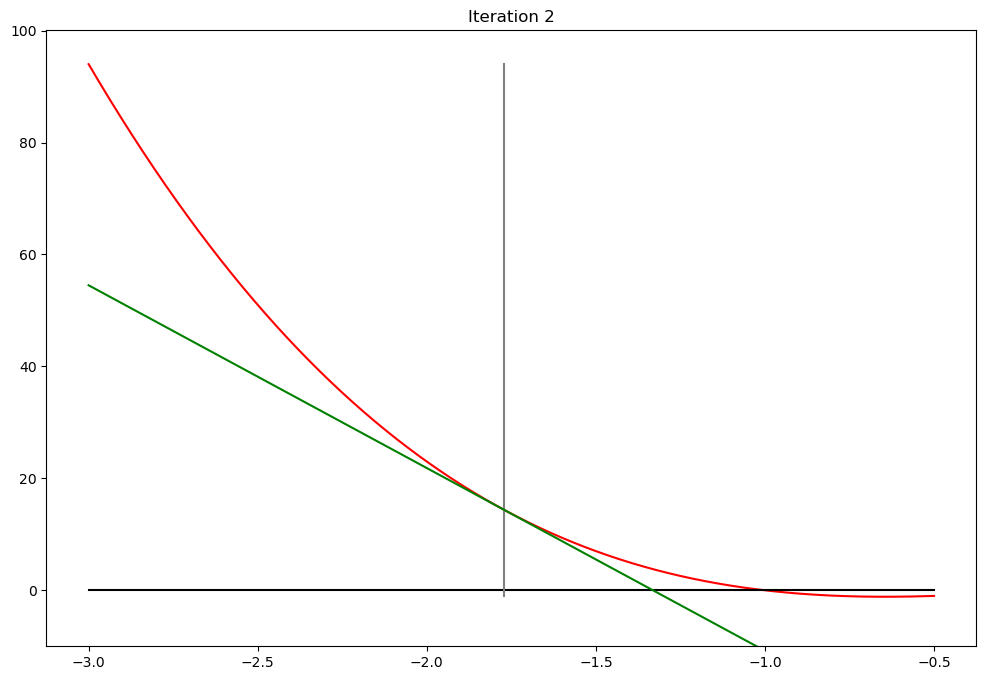
Converged in 7 steps

Rate of convergence of the two methods

• How fast does a solution method converge on the root of the equation?

• Rate of convergence = the rate of decrease of the bias (difference between current guess and the solution)

• Can be approximated by the rate of decrease of the error in the stopping criterion

Bisections: linear convergence

Newton: quadratic convergence

def print_err(iter,err,**kwargs):
    x = kwargs['x'] if 'x' in kwargs.keys() else kwargs['x0']
    print('{:4d}:  x = {:17.14f}  err = {:8.6e}'.format(iter,x,err))

print('Newton method')
newton(f,g,x0=-2.5,callback=print_err,tol=1e-10)

print('Bisection method')
bisection(f,a=-3,b=-0.5,callback=print_err,tol=1e-10)

Newton method
   0:  x = -2.50000000000000  err = 7.285714e-01
   1:  x = -1.77142857142857  err = 4.402791e-01
   2:  x = -1.33114944950557  err = 2.323743e-01
   3:  x = -1.09877514383983  err = 8.562251e-02
   4:  x = -1.01315263007170  err = 1.286646e-02
   5:  x = -1.00028616796687  err = 2.860277e-04
   6:  x = -1.00000014027560  err = 1.402756e-07
   7:  x = -1.00000000000003  err = 3.375078e-14
Bisection method
   0:  x = -1.75000000000000  err = 2.500000e+00
   1:  x = -1.12500000000000  err = 1.250000e+00
   2:  x = -0.81250000000000  err = 6.250000e-01
   3:  x = -0.96875000000000  err = 3.125000e-01
   4:  x = -1.04687500000000  err = 1.562500e-01
   5:  x = -1.00781250000000  err = 7.812500e-02
   6:  x = -0.98828125000000  err = 3.906250e-02
   7:  x = -0.99804687500000  err = 1.953125e-02
   8:  x = -1.00292968750000  err = 9.765625e-03
   9:  x = -1.00048828125000  err = 4.882812e-03
  10:  x = -0.99926757812500  err = 2.441406e-03
  11:  x = -0.99987792968750  err = 1.220703e-03
  12:  x = -1.00018310546875  err = 6.103516e-04
  13:  x = -1.00003051757812  err = 3.051758e-04
  14:  x = -0.99995422363281  err = 1.525879e-04
  15:  x = -0.99999237060547  err = 7.629395e-05
  16:  x = -1.00001144409180  err = 3.814697e-05
  17:  x = -1.00000190734863  err = 1.907349e-05
  18:  x = -0.99999713897705  err = 9.536743e-06
  19:  x = -0.99999952316284  err = 4.768372e-06
  20:  x = -1.00000071525574  err = 2.384186e-06
  21:  x = -1.00000011920929  err = 1.192093e-06
  22:  x = -0.99999982118607  err = 5.960464e-07
  23:  x = -0.99999997019768  err = 2.980232e-07
  24:  x = -1.00000004470348  err = 1.490116e-07
  25:  x = -1.00000000745058  err = 7.450581e-08
  26:  x = -0.99999998882413  err = 3.725290e-08
  27:  x = -0.99999999813735  err = 1.862645e-08
  28:  x = -1.00000000279397  err = 9.313226e-09
  29:  x = -1.00000000046566  err = 4.656613e-09
  30:  x = -0.99999999930151  err = 2.328306e-09
  31:  x = -0.99999999988358  err = 1.164153e-09
  32:  x = -1.00000000017462  err = 5.820766e-10
  33:  x = -1.00000000002910  err = 2.910383e-10
  34:  x = -0.99999999995634  err = 1.455192e-10

-0.9999999999563443

Measuring complexity of Newton and bisection methods

• What is the size of input \( n \)?

• Desired precision of the solution!

• Thus, attention to the errors in the solution as algorithm proceeds

• Rate of convergence is part of the computational complexity of the algorithms

Computational complexity of Newton method

• Calculating a root of a function f(x) with n-digit precision

• Provided that a good initial approximation is known

• Is \( O((logn)F(n)) \), where \( F(n) \) is the cost of

• calculating \( f(x)/f'(x) \) with \( n \)-digit precision

Further learning resources

• On computational complexity of Newton method https://m.tau.ac.il/~tsirel/dump/Static/knowino.org/wiki/Newton’s_method.html#Computational_complexity

• “Improved convergence and complexity analysis of Newton’s method for solving equations” https://www.tandfonline.com/doi/abs/10.1080/00207160601173431?journalCode=gcom20